题目内容
9.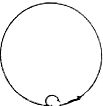 光滑绝缘的圆形轨道竖直放置,半径为R,在其最低点A处放一质量为m的带电小球,整个空间存在匀强电场,小球受到的电场力大小为mg,方向水平向右,现给小球一个水平向右的初速度v0,使小球沿轨道向上运动,若小球刚好能做完整的圆周运动,求v0大小(计算结果可以保留根号)
光滑绝缘的圆形轨道竖直放置,半径为R,在其最低点A处放一质量为m的带电小球,整个空间存在匀强电场,小球受到的电场力大小为mg,方向水平向右,现给小球一个水平向右的初速度v0,使小球沿轨道向上运动,若小球刚好能做完整的圆周运动,求v0大小(计算结果可以保留根号)
分析 小球在圆形轨道内做圆周运动,如果小球能经过小球所受合力反方向的最高点,则小球可以做完整的圆周运动,应用牛顿第二定律求出小球在等效最高点的临界速度,然后应用动能定理求出小球的初速度.
解答 解:小球所受合力:F=$\sqrt{(mg)^{2}+(qE)^{2}}$=$\sqrt{2}$mg,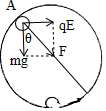
tanθ=$\frac{qE}{mg}$=$\frac{mg}{mg}$=1,解得:θ=45°,
小球恰好做完整的圆周运动,在等效最高点A,
由牛顿第二定律得:F=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{\sqrt{2}gR}$,
小球从最低点到A点过程,由动能定理得:
-FR-FRcosθ=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02,
解得:v0=$\sqrt{(3\sqrt{2}+2)gR}$;
答:v0大小为$\sqrt{(3\sqrt{2}+2)gR}$.
点评 本题考查了求小球速度大小,分析清楚小球的运动过程、找出等效最高点是解题的前提与关键,应用动能定理与牛顿第二定律可以解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.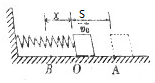 如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
 如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )
如图所示,质量为m的物块将劲度系数为k的弹簧压缩到B点并锁定,弹簧的压缩量为x.弹簧原长位置为O点,O点左边水平面光滑,O点右边水平面的动摩擦因数为μ,某时刻解锁后物块在弹簧弹力的作用下向右运动,经O点时的速度为v0,物块最终停止在距离O右边S米的A点,则开始时弹簧的弹性势能多大( )| A. | $\frac{1}{2}m{v}_{0}^{2}$ | B. | $\frac{1}{2}$kx2 | C. | kx2 | D. | μmgS |
17.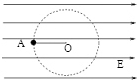 如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
 如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )
如图,匀强电场水平向右,细线一端固定,另一端拴一带正电小球.使球在竖直面内绕固定端O做圆周运动,不计空气阻力,静电力和重力大小刚好相等,细线长为r,当小球运动到图中位置A时,细线在水平方向,拉力大小Fr=3mg,重力加速度大小为g,则小球的最小速度大小为( )| A. | $\sqrt{2gr}$ | B. | 2$\sqrt{gr}$ | C. | $\sqrt{(6-2\sqrt{2})gr}$ | D. | $\sqrt{(6+2\sqrt{2})gr}$ |
4. 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
 如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一质量为m、带电荷量为q的物体处于场强按E=kt(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间动摩擦因数为μ,当t=0时刻将物体从静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )| A. | 物体开始运动后加速度大小可以大于g | |
| B. | 物体开始运动后加速度不断减小 | |
| C. | 经过时间t=$\frac{mg}{μkq}$,物体在竖直墙壁上的位移达到最大值 | |
| D. | 经过时间t=$\frac{mg}{μkq}$,物体运动速度达最大值 |
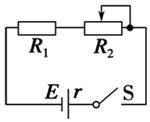 如图,已知E=8V,r=4Ω,R1=2Ω,R2的变化范围是0-10Ω.求:
如图,已知E=8V,r=4Ω,R1=2Ω,R2的变化范围是0-10Ω.求: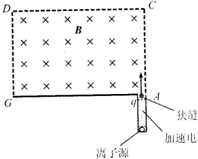 利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.
利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.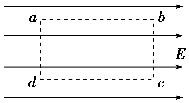 如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J.
如图所示的匀强电场场强为103 N/C,沿电场线方向ab=dc=4cm垂直电场线方向bc=ad=3cm.则ab之间的电势差为40V,若将q=-5×10-3 C的点电荷沿矩形路径abcd移动一周,电场力做功是0J.