题目内容
10．
如图滑雪者从高8m的山坡上的A点由静止下滑，最后停止在C点，A、C两点的水平距离为s=100m，求滑雪者与雪面间的动摩擦因数．
分析 对AC运动过程应用动能定理求解．
解答 解：设斜面与水平面交点为B，那么AC运动过程作用重力、摩擦力做功，由动能定理可得：
$mgh-μmgcosθ•\frac{h}{sinθ}-μmgBC=0$；
$mgh-μmg（\frac{h}{tanθ}+BC）=mgh-μmgs=0$
解得：$μ=\frac{h}{s}=0.08$；
答：滑雪者与雪面间的动摩擦因数0.08．
点评 经典力学问题一般先对物体进行受力分析，求得合外力及运动过程做功情况，然后根据牛顿定律、动能定理及几何关系求解．
练习册系列答案
相关题目
取一对用绝缘柱支持导体A和B，使它们彼此接触．起初它们不带电，贴在下部的金属箔是闭合的（如图）．
1．
如图所示，一根绳子一端固定于竖直墙上的A点，另一端绕过动滑轮P悬挂一重物B，其中绳子的PA段处于水平状态，另一根绳子一端与动滑轮P的轴相连，绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F，使整个系统处于平衡状态，滑轮均为光滑、轻质，且均可看做质点，现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态，则该平衡状态与原平衡状态相比较（ ）
如图所示，一根绳子一端固定于竖直墙上的A点，另一端绕过动滑轮P悬挂一重物B，其中绳子的PA段处于水平状态，另一根绳子一端与动滑轮P的轴相连，绕过光滑的定滑轮Q后在其端点O施加一水平向左的外力F，使整个系统处于平衡状态，滑轮均为光滑、轻质，且均可看做质点，现拉动绳子的端点O使其向左缓慢移动一小段距离后达到新的平衡状态，则该平衡状态与原平衡状态相比较（ ）| A． | 拉力F增大 | B． | 角θ减小 | C． | 拉力FPA不变 | D． | 角θ不变 |
山地滑雪是人们喜爱的一项体育运动．一雪坡由AB和BC两段组成，AB是倾角为θ=37°的斜坡，可认为光滑．BC是半径为R=5m的圆弧面，有摩擦．圆弧面BC与斜坡AB相切于B点，与水平面相切于C点，如图所示．又已知AB竖直高度h1=5m，运动员连同滑雪装备总质量为80kg，从A点由静止滑下通过C点后飞落到DE上，其中运动员在BC圆弧面上运动时由于受到摩擦力的作用速度的大小保持不变．整个运动过程中不计空气阻力，g取10m/s2，sin37°=0.6，cos37°=0.8．求：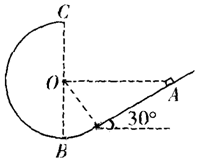
如图所示，竖直平面内一半径为R的光滑圆弧形内轨道与倾角θ=30°的粗糙斜面连接，连接处与光滑圆弧相切，质量为m，可视为质点的物块从斜面上与圆心等高的A点以初速度v0滑下，经过圆心正上方的轨道最高点C抛出后，恰又落到A点．设物块与斜面间动摩擦因数μ=0.2，重力加速度为g，求：
如图所示，ABC为一个竖直固定的半径为R的四分之三圆环管道，管道内壁光滑，内径远远小于圆环半径，计算中可以忽略，DE是一个光滑的水平桌面．质量为m的小球直径略小于管道内径，通过一根穿过管道的轻线连接一质量为3m的物块．初开始物块在桌面上位于C点正下方的P点，小球在管道最低点A处，线处于张紧状态，测得线的总长度为L=$\frac{5}{2}$πR，现在突然给物块一个水平向左的初速度，物块将向左运动而带动小球上升，当小球到达最高点B时，管道的外壁对小球有一个向内的大小为N=3mg的弹力．
19．水平放置的机枪，枪管水平，机枪总质量为M，子弹的质量为m、当它以速度v射出n颗子弹时，机枪获得的反向速度为（ ）
| A． | $\frac{nm}{M-nm}$v | B． | -$\frac{nm}{M-nm}$v | C． | $\frac{nm}{M+nm}$v | D． | -$\frac{nm}{M+nm}$v |
