��Ŀ����
10��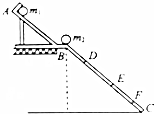 Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ��ijͬѧѡȡ�����������ͬ���������ȵ�С������������ʵ�飺
Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ��ijͬѧѡȡ�����������ͬ���������ȵ�С������������ʵ�飺������ƽ�������С��������ֱ�Ϊm1��m2����m1��m2��
�ڰ�����ͼ��ʾ����װ��ʵ��װ�ã���б��AB�̶������ߣ�ʹ�۵�ĩ��ˮƽ����һб��BC������б��ĩ�ˣ�
���Ȳ���С��m2����С��m1��б�۶���A���ɾ�ֹ��ʼ���£�����С����б��������λ�ã�
�ܽ�С��m2����б��ĩ��B������С��m1��б�۶���A�����£�ʹ���Ƿ�����ײ������С��m1��С��m2��б��������λ�ã�
���ú��̶ȳ�������������λ�õ�б��ĩ��B�ľ��룮ͼ��D��E��F���Ǹ�ͬѧ���µ�С����б���ϵļ�������λ�ã���B��ľ���ֱ�ΪLD��LE��LF��
б����ƽ�����Ӵ�����������ʧ�����ݸ�ͬѧ��ʵ�飬�ش��������⣺
��1��С��m1��m2������ײ��m1�������ͼ�е�D�㣬m2�������ͼ�е�F�㣮
��2���ò�õ�����������ʾ��ֻҪ�����ϵʽm1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$����˵����ײ�ж������غ�ģ�
��3���ò�õ�����������ʾ��ֻҪ�����ϵʽm1LE=m1LD+m2LF����˵����С�����ײ�ǵ�����ײ��
���� ��1��С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶�����ƽ���˶����ɲ����жϳ���
��2����б��BC��ˮƽ������Ϊ������ƽ���˶����������ײǰ��С��m1��С��m2���ٶȣ���ʾ�������ı���ʽ������⣻
��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ�����ݻ�е���غ㶨�ɿ���ñ���ʽ��
��� �⣺��1��С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶���������ײ��m1�����ص���D�㣬m2�����ص���F�㣻
��2����ײǰ��С��m1����ͼ�е�E�㣬����ˮƽ���ٶ�Ϊv1��С��m1��m2������ײ��m1�������ͼ�е�D�㣬����ˮƽ���ٶ�Ϊv1�䣬m2�������ͼ�е�F�㣬����ˮƽ���ٶ�Ϊv2�� ��б��BC��ˮƽ������Ϊ����
��ƽ���˶����ɵã�LDsin��=$\frac{1}{2}$gt2��LDcos��=v��1t
��ã�v��1=$\sqrt{\frac{g{L}_{D}��cos����^{2}}{2sin��}}$��ͬ���ɽ�ã�v1=$\sqrt{\frac{g{L}_{E}��cos����^{2}}{2sin��}}$��v2=$\sqrt{\frac{g{L}_{F}��cos����^{22}}{2sin��}}$��
����ֻҪ����m1v1=m2v2+m1v��1������m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$�� ��˵��������ײ�����ж����غ㣻
��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ��
��Ҫ�����ϵʽ��$\frac{1}{2}$m1v12=$\frac{1}{2}$m1v��12+$\frac{1}{2}$m2v2����m1LE=m1LD+m2LF��
�ʴ�Ϊ����1��D��F����2��m1$\sqrt{{L}_{E}}$=m1$\sqrt{{L}_{D}}$+m2$\sqrt{{L}_{F}}$����3��m1LE=m1LD+m2LF��
���� ��������ƽ���˶��Ĺ��ɿ��鶯���غ㶨�ɵ���֤����Ŀ��Ϊ��ӱ��Ҫѧ������ƽ���˶��Ļ������������ײǰ����ٶȣ��Ӷ���֤�����غ㶨�ɣ�ͬʱע����С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ��

 �����У����ſ��ñȽϽ��ĺ��ǣ�ֻ�ܵ��˴�֮��������������û�����ת����֮Ϊ˫��ϵͳ���ں�嫵�����ϵ�У��������Ƕ���˫��ϵͳ����ij˫��ϵͳP��Q���������ϵ�O��������Բ���˶�����ͼ��ʾ����PO��OQ��������
�����У����ſ��ñȽϽ��ĺ��ǣ�ֻ�ܵ��˴�֮��������������û�����ת����֮Ϊ˫��ϵͳ���ں�嫵�����ϵ�У��������Ƕ���˫��ϵͳ����ij˫��ϵͳP��Q���������ϵ�O��������Բ���˶�����ͼ��ʾ����PO��OQ��������| A�� | ����P������һ������Q������ | |
| B�� | ����P�����ٶ�һ������Q�����ٶ� | |
| C�� | ˫�Ǽ����һ����˫�ǵ�����Խ����ת������Խ�� | |
| D�� | ˫�ǵ�����һ����˫��֮��ľ���Խ����ת������Խ�� |
 ��ͼ��ʾ�����53��Ĵֲ�б��̶���ˮƽ���ϣ�һ����Ϊm1��С����A����б���ϣ������̶���б�涥�˵Ĺ⻬�����ֵ�������������������һ��������Ϊm2��С����B���ӣ�B�����̶��ڵ����ϵ���ֱ�⻬�ˣ����������̶�B����ʱ����B�����IJ��ִ���ˮƽ��ֱ״̬����A�����IJ�����б��ƽ�У��ɾ�ֹ�ͷ�B��B����A��б�������˶���������B�����IJ�����ˮƽ����ļн�37��ʱ��B���ٶ�Ϊv����ʱA��û�е���б�涥�ˣ���֪m1=m0��m2=3m0���⻬��������˵ļ��ΪL�����ڴ˹����У�sin37��=cos53��=0.6��cos37��=sin53��=0.8����������
��ͼ��ʾ�����53��Ĵֲ�б��̶���ˮƽ���ϣ�һ����Ϊm1��С����A����б���ϣ������̶���б�涥�˵Ĺ⻬�����ֵ�������������������һ��������Ϊm2��С����B���ӣ�B�����̶��ڵ����ϵ���ֱ�⻬�ˣ����������̶�B����ʱ����B�����IJ��ִ���ˮƽ��ֱ״̬����A�����IJ�����б��ƽ�У��ɾ�ֹ�ͷ�B��B����A��б�������˶���������B�����IJ�����ˮƽ����ļн�37��ʱ��B���ٶ�Ϊv����ʱA��û�е���б�涥�ˣ���֪m1=m0��m2=3m0���⻬��������˵ļ��ΪL�����ڴ˹����У�sin37��=cos53��=0.6��cos37��=sin53��=0.8����������| A�� | B���ٵ���������Ϊ$\frac{9}{4}$m0gL | |
| B�� | A���ӵ���������Ϊ$\frac{3}{4}$m0gL | |
| C�� | A���ӵĶ���Ϊ$\frac{1}{2}$m0v2 | |
| D�� | A��B����ɵ�ϵͳ��ʧ�Ļ�е��Ϊ$\frac{41}{20}$m0gL-$\frac{42}{25}$m0v2 |
 �ҹ�Ԥ����2017��ǰ�����϶���ţ�ʵ������ȡ�������ص�����Ŀǰ����Ʒ������϶�����ɹ��������½���ȶ��������ɣ���½��Я����Ʒ������������գ����ڽ���Բ����������У��������������ϸ߹�����ϵĹ�����Խӣ�����ɹ����Я����Ʒ���ص������й��ڴ˹�����˵����ȷ���ǣ�������
�ҹ�Ԥ����2017��ǰ�����϶���ţ�ʵ������ȡ�������ص�����Ŀǰ����Ʒ������϶�����ɹ��������½���ȶ��������ɣ���½��Я����Ʒ������������գ����ڽ���Բ����������У��������������ϸ߹�����ϵĹ�����Խӣ�����ɹ����Я����Ʒ���ص������й��ڴ˹�����˵����ȷ���ǣ�������| A�� | ��½���ڢ����Ķ��ܱض����ڢ����Ķ��� | |
| B�� | ��½���ڢ����Ļ�е��С���ڢ����Ļ�е�� | |
| C�� | ��½��Ӧͨ�����ٵ�������Ӷ�ʵ���������Խ� | |
| D�� | ��½��Ӧ�ȵ��������Ȼ����ǰ���ٶȼ��٣������Ϲ����ʵ�ֶԽ� |
 Ϊ�˲��������ڸɵ����ɵĵ����ĵ綯�ƺ��ڵ��裮ijͬѧ��ʵ���������������ģ�
Ϊ�˲��������ڸɵ����ɵĵ����ĵ綯�ƺ��ڵ��裮ijͬѧ��ʵ���������������ģ� ��ͼ��AB�Ǹ�h1=0.8m����Ǧȵ�б�棬������ˮƽ�����ϣ�б���¶������������е�һ��Բ�����ҽ������ӱ�Ե��һ������m=1.0kg��С����ӹ⻬б�涥��A�ɾ�ֹ��ʼ�ع���»����˶���б���Bʱ��ˮƽ�����뿪б�棬�䵽ˮƽ�����ϵ�C�㣬��ص�C�����ӱ�Ե��ˮƽ����2.4m�����ƿ�����������g=10m/s2��ȡ����Ϊ�ο�ƽ�棩
��ͼ��AB�Ǹ�h1=0.8m����Ǧȵ�б�棬������ˮƽ�����ϣ�б���¶������������е�һ��Բ�����ҽ������ӱ�Ե��һ������m=1.0kg��С����ӹ⻬б�涥��A�ɾ�ֹ��ʼ�ع���»����˶���б���Bʱ��ˮƽ�����뿪б�棬�䵽ˮƽ�����ϵ�C�㣬��ص�C�����ӱ�Ե��ˮƽ����2.4m�����ƿ�����������g=10m/s2��ȡ����Ϊ�ο�ƽ�棩 ��ͼ��ʾ��һ��ˮƽ���D�ĵ������ף�����һ�˿��ڣ�һ�η�գ����ȵĻ����������ڿ�����Ħ���Ļ���������������֮���ܷ���ã����ײ������֮���ܷ���һ���������������壬���¶�ΪT�������ĺ�����ΪS�������������ײ�ΪL���������ز�����ѹǿΪO.5P0����ʱ���������ھ�ֹ״̬�������ѹǿΪP0����绷���¶Ȳ��䣮
��ͼ��ʾ��һ��ˮƽ���D�ĵ������ף�����һ�˿��ڣ�һ�η�գ����ȵĻ����������ڿ�����Ħ���Ļ���������������֮���ܷ���ã����ײ������֮���ܷ���һ���������������壬���¶�ΪT�������ĺ�����ΪS�������������ײ�ΪL���������ز�����ѹǿΪO.5P0����ʱ���������ھ�ֹ״̬�������ѹǿΪP0����绷���¶Ȳ��䣮