题目内容
1.我国“嫦娥三号”探月卫星已成功发射,设卫星距月球表面的高度为h,做匀速圆周运动的周期为T,已知月球半径为R,引力常量为G,求:(1)月球表面的重力加速度g
(2)月球的第一宇宙速度v.
分析 (1)根据万有引力提供向心力,结合卫星的轨道半径和周期求出月球的质量.由万有引力等于重力求得加速度g,
(2)根据重力提供向心力可确定其第一宇宙速度.
解答 解:(1)根据$G\frac{Mm}{(R+h)^{2}}=m(R+h)\frac{4{π}^{2}}{{T}^{2}}$解得月球的质量为:M=$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$,
表面的重力加速度为:g=$\frac{GM}{{R}^{2}}$=$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$
(2)第一宇宙速度为v,由mg=$m\frac{{v}^{2}}{R}$得:$v=\sqrt{gR}$=$\frac{2π(R+h)}{T}\sqrt{\frac{R+h}{R}}$
答:(1)月球表面的重力加速度为$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$
(2)月球的第一宇宙速度为$\frac{2π(R+h)}{T}\sqrt{\frac{R+h}{R}}$.
点评 解决本题的关键掌握万万有引力等于重力,能正确根据卫星运动时的向心力由万有引力提供列出等式求解,第一宇宙速度也是近星的环绕速度.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
13. 如图所示,一个人把质量为m的石块,从距地面高度为h处,以初速度v0斜向上方抛出.以水平地面处为势能零点,不计空气阻力,重力加速度为g,则( )
如图所示,一个人把质量为m的石块,从距地面高度为h处,以初速度v0斜向上方抛出.以水平地面处为势能零点,不计空气阻力,重力加速度为g,则( )
 如图所示,一个人把质量为m的石块,从距地面高度为h处,以初速度v0斜向上方抛出.以水平地面处为势能零点,不计空气阻力,重力加速度为g,则( )
如图所示,一个人把质量为m的石块,从距地面高度为h处,以初速度v0斜向上方抛出.以水平地面处为势能零点,不计空气阻力,重力加速度为g,则( )| A. | 石块离开手的时刻机械能为$\frac{1}{2}$mv02 | B. | 石块刚落地的时刻动能为mgh | ||
| C. | 人对石块做的功是$\frac{1}{2}$mv02+mgh | D. | 人对石块做的功是$\frac{1}{2}$mv02 |
16.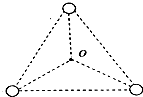 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )| A. | 每个星体受到向心力大小均为3$\frac{G{m}^{2}}{{a}^{2}}$ | |
| B. | 每个星体的角速度均为$\sqrt{\frac{3Gm}{{a}^{2}}}$ | |
| C. | 若a不变,m是原来的两倍,则周期是原来的$\frac{1}{2}$ | |
| D. | 若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$ |
6. 如图,P、Q两个完全相同的物体放在车上,且相对于小车静止,一起水平向右做匀加速直线运动,运动中小车对P、Q的作用力相比较( )
如图,P、Q两个完全相同的物体放在车上,且相对于小车静止,一起水平向右做匀加速直线运动,运动中小车对P、Q的作用力相比较( )
 如图,P、Q两个完全相同的物体放在车上,且相对于小车静止,一起水平向右做匀加速直线运动,运动中小车对P、Q的作用力相比较( )
如图,P、Q两个完全相同的物体放在车上,且相对于小车静止,一起水平向右做匀加速直线运动,运动中小车对P、Q的作用力相比较( )| A. | 它们方向相同,都水平向右 | B. | 它们方向相同且都不沿水平方向 | ||
| C. | 它们方向不同,其中一个沿水平方 | D. | 它们方向不同,且都不沿水平方向 |
13.一个做匀速直线运动的物体,从某时刻起受到一个运动方向不在同一直线上的恒力作用.在此之后,物体( )
| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 可能做匀速圆周运动 | D. | 运动速度大小一定不断增大 |
11.国家体育总局会同国家环保部门从2010年初开始对将在广州进行的亚运会的所有场馆分期进行验收,其中有一项为放射性污染检测,因为建筑材料,如水泥、砖、混凝土中含有为了体现绿色奥运放射性元素氧.下列有关放射性的说法中正确的有( )
| A. | ${\;}_{90}^{238}U$衰变成20682pb要经过8次α衰变和6次β衰变 | |
| B. | 氧发生α衰变产生的α粒子是一种高速电子流,具有很强的穿透能力 | |
| C. | 放射性元素发生β衰变时所释放的电子是原子核内的中子转化为质子时产生的 | |
| D. | β射线与γ射线一样是电磁波,但穿透本领远比γ射线小 |
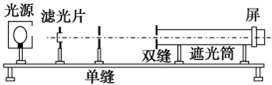
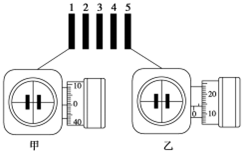
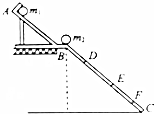 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不等的小球.按下述步骤做实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不等的小球.按下述步骤做实验: