题目内容
11.某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,春分那天(太阳光直射赤道)在日落后的12小时内有t1时间该观察者看不见此卫星.已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,卫星的绕行方向与地球转动方向相同,不考虑大气对光的折射.下列说法中正确的是( )| A. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{2{π}^{2}}}$ | |
| B. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | |
| C. | t1=$\frac{T}{π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ | |
| D. | t1=$\frac{T}{2π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ |
分析 同步卫星绕地球做匀速圆周运动,受到的万有引力提供向心力,其向心力用周期表示,结合“黄金代换”求出同步卫星的轨道半径,再利用几何关系确定太阳照不到同步卫星的范围,那么,即可求出看不到卫星的时间.
解答 解:A、设地球同步卫星的轨道半径为r,其受到的地球万有引力提供向心力,即:$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$,
对地面上的物体万有引力等于重力有:$G\frac{Mm}{{R}^{2}}=mg$,
由以上两式可得:r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$,
所以同步卫星离地高度为h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R.故A错误,B正确;
C、根据光的直线传播规律,日落12小时内有t1时间该观察者看不见此卫星图示如图所示,
同步卫星相对地心转过角度为θ=2α,sinα=$\frac{R}{r}$,
结合θ=ωt=$\frac{2π}{T}$t,
解得:t1=$\frac{T}{π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$,故C正确,D错误;
故选:BC
点评 解决天体问题把握两条思路:一是万有引力提供向心力,二是重力等于万有引力.针对本题关键还要分析好几何关系来求解.

练习册系列答案
相关题目
15.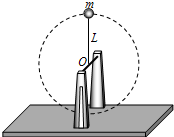 如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )
如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )
 如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )
如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )| A. | 运动过程中小球的最小速度为$\sqrt{\frac{MgL}{m}}$ | |
| B. | 运动过程中绳的最大拉力为6mg+Mg | |
| C. | 运动过程中小球的最大瞬时角速度为$\sqrt{\frac{(M+m)g}{mL}+\frac{2g}{L}}$ | |
| D. | 当绳处于水平时地面对底座的摩擦力为Mg+2mg |
2.甲物体的重力是乙物体的3倍,它们在某地从同一高度处同时做自由落体运动,则下列说法中正确的是( )
| A. | 甲比乙先着地 | B. | 甲、乙同时着地 | C. | 乙的速度比甲大 | D. | 甲的速度比乙大 |
19. 据报道,一个国际研究小组借助于智利的天文望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质,达到质量转移的目的,在演变过程中两者球心之间的距离保持不变,双星平均密度可视为相同.则在最初演变的过程中( )
据报道,一个国际研究小组借助于智利的天文望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质,达到质量转移的目的,在演变过程中两者球心之间的距离保持不变,双星平均密度可视为相同.则在最初演变的过程中( )
 据报道,一个国际研究小组借助于智利的天文望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质,达到质量转移的目的,在演变过程中两者球心之间的距离保持不变,双星平均密度可视为相同.则在最初演变的过程中( )
据报道,一个国际研究小组借助于智利的天文望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质,达到质量转移的目的,在演变过程中两者球心之间的距离保持不变,双星平均密度可视为相同.则在最初演变的过程中( )| A. | 它们做圆周运动的万有引力保持不变 | |
| B. | 它们做圆周运动的角速度不断变小 | |
| C. | 体积较大的星体圆周运动轨迹的半径变大,线速度变大 | |
| D. | 体积较大的星体圆周运动轨迹的半径变小,线速度变大 |
16. 如图所示,一列沿负x方向传播的简谐横波,图示时刻为t=0时刻的波动图象,a、b、c、d、e分别是xa=2m,xb=4m,xc=6m,xd=7m,xe=9m处的五个质点,已知波的传播速度为2m/s,则在第2秒内回复力做功相同的两个质点是( )
如图所示,一列沿负x方向传播的简谐横波,图示时刻为t=0时刻的波动图象,a、b、c、d、e分别是xa=2m,xb=4m,xc=6m,xd=7m,xe=9m处的五个质点,已知波的传播速度为2m/s,则在第2秒内回复力做功相同的两个质点是( )
 如图所示,一列沿负x方向传播的简谐横波,图示时刻为t=0时刻的波动图象,a、b、c、d、e分别是xa=2m,xb=4m,xc=6m,xd=7m,xe=9m处的五个质点,已知波的传播速度为2m/s,则在第2秒内回复力做功相同的两个质点是( )
如图所示,一列沿负x方向传播的简谐横波,图示时刻为t=0时刻的波动图象,a、b、c、d、e分别是xa=2m,xb=4m,xc=6m,xd=7m,xe=9m处的五个质点,已知波的传播速度为2m/s,则在第2秒内回复力做功相同的两个质点是( )| A. | a和b | B. | b和c | C. | c和d | D. | d和e |
3. 如图所示,一细光束从空气经界面EE'折射入平行玻璃砖,由界面FF′出射至空气时分为了a、b两束.下列说法正确的是( )
如图所示,一细光束从空气经界面EE'折射入平行玻璃砖,由界面FF′出射至空气时分为了a、b两束.下列说法正确的是( )
 如图所示,一细光束从空气经界面EE'折射入平行玻璃砖,由界面FF′出射至空气时分为了a、b两束.下列说法正确的是( )
如图所示,一细光束从空气经界面EE'折射入平行玻璃砖,由界面FF′出射至空气时分为了a、b两束.下列说法正确的是( )| A. | 出射的a、b光必平行 | |
| B. | 在玻璃中,a光的传播速度大于b光的传播速度 | |
| C. | 若增大入射角θ(θ<90°),在FF′下侧,出射光a、b 将先后消失 | |
| D. | 若用a、b光分别照射同-双缝干涉装置,在屏上,a光形成的条纹间距大于b光形成的条纹间距 |
1.探月工程三期飞行试验器于2014年100月24日2时在中国西昌卫星发射中心发射升空,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始在月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列选项正确的是( )
| A. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{R}{R+h}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |
 在描绘小灯泡的伏安特性曲线的实验中,已知待测小灯泡的额定电压6V,额定功率为3W,提供的器材有:
在描绘小灯泡的伏安特性曲线的实验中,已知待测小灯泡的额定电压6V,额定功率为3W,提供的器材有: 某学习小组为了研究标有“2.5V 0.3A”字样小灯泡的伏安特性曲线,到实验室找到了下列器材:
某学习小组为了研究标有“2.5V 0.3A”字样小灯泡的伏安特性曲线,到实验室找到了下列器材: