题目内容
1.探月工程三期飞行试验器于2014年100月24日2时在中国西昌卫星发射中心发射升空,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始在月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列选项正确的是( )| A. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{R}{R+h}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |
分析 根据万有引力与星球表面重力相等列出等式,根据牛顿第二定律得出飞行试验器在工作轨道上的加速度;
飞行器绕月运行时万有引力提供圆周运动向心力列出等式求解;
根据万有引力提供向心力,推导出线速度求解;
根据密度定义求解.
解答 解:令月球质量为M,在月球表面重力与万有引力相等有:$\frac{GmM}{{R}^{2}}$=mg,
可得:GM=gR2
A、万有引力提供向心力,有:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$=ma
v=$\sqrt{\frac{GM}{r}}$=R$\sqrt{\frac{g}{R+h}}$,故A正确;
B、飞行试验器工作轨道处的重力加速度为g′=$\frac{GM}{{r}^{2}}$=($\frac{R}{R+h}$)2g,故B正确;
C、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$=2π$\sqrt{\frac{{(R+h)}^{3}}{{gR}^{2}}}$,故C错误;
D、月球的密度ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{3g}{4πGR}$,故D正确;
故选:ABD
点评 万有引力提供圆周运动向心力和万有引力与星球表面重力相等是解决此类问题的主要入手点,关键是掌握相关公式及公式变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,春分那天(太阳光直射赤道)在日落后的12小时内有t1时间该观察者看不见此卫星.已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,卫星的绕行方向与地球转动方向相同,不考虑大气对光的折射.下列说法中正确的是( )
| A. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{2{π}^{2}}}$ | |
| B. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | |
| C. | t1=$\frac{T}{π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ | |
| D. | t1=$\frac{T}{2π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ |
12.电流传感器可以像电流表一样测量电流,不同的是,它的反应非常快,可以捕捉到瞬间的电流变化.此外,由于它与计算机相连,能在几秒内画出电流随时间变化的图象.现照图甲连接电路,先使开关S与1端相连,电源向电容器充电,这个过程可在瞬间完成.然后把开关S掷向2端,电容器通过电阻R放电,传感器将电流信息传入计算机,屏幕上显示出电流随时间变化的I-t曲线.一同学想利用I-t曲线图象估算电容器的电容大小,还需提供哪个物理量( )


| A. | 电源的电动势E | B. | 电容器两极板的距离d | ||
| C. | 电容器两极板的正对面积S | D. | 电容器两极板间的电介质ε |
16. 2015年为纪念中国人民抗日战争暨世界反法西斯战争胜利70周年,中央电视台6频道播出了抗战经典影片《地雷战》,吸引了一大批90后高中生的观看.小陈同学看了其中日本工兵探雷的片段后,自己制做了一个简易的金属探测器,如图所示.E是一个有不变内阻的电源,A和V均是理想电表,R0为一特殊电阻,能让电路中的电流在一个工作周期内均匀增大,检测报警装置非常灵敏且电阻恒定,在一个工作周期内,检测到电路中的电流不是均匀增大时能报警.L是电阻不计的单匝线圈,忽略L的自感,则闭合开关,在一个工作周期内( )
2015年为纪念中国人民抗日战争暨世界反法西斯战争胜利70周年,中央电视台6频道播出了抗战经典影片《地雷战》,吸引了一大批90后高中生的观看.小陈同学看了其中日本工兵探雷的片段后,自己制做了一个简易的金属探测器,如图所示.E是一个有不变内阻的电源,A和V均是理想电表,R0为一特殊电阻,能让电路中的电流在一个工作周期内均匀增大,检测报警装置非常灵敏且电阻恒定,在一个工作周期内,检测到电路中的电流不是均匀增大时能报警.L是电阻不计的单匝线圈,忽略L的自感,则闭合开关,在一个工作周期内( )
 2015年为纪念中国人民抗日战争暨世界反法西斯战争胜利70周年,中央电视台6频道播出了抗战经典影片《地雷战》,吸引了一大批90后高中生的观看.小陈同学看了其中日本工兵探雷的片段后,自己制做了一个简易的金属探测器,如图所示.E是一个有不变内阻的电源,A和V均是理想电表,R0为一特殊电阻,能让电路中的电流在一个工作周期内均匀增大,检测报警装置非常灵敏且电阻恒定,在一个工作周期内,检测到电路中的电流不是均匀增大时能报警.L是电阻不计的单匝线圈,忽略L的自感,则闭合开关,在一个工作周期内( )
2015年为纪念中国人民抗日战争暨世界反法西斯战争胜利70周年,中央电视台6频道播出了抗战经典影片《地雷战》,吸引了一大批90后高中生的观看.小陈同学看了其中日本工兵探雷的片段后,自己制做了一个简易的金属探测器,如图所示.E是一个有不变内阻的电源,A和V均是理想电表,R0为一特殊电阻,能让电路中的电流在一个工作周期内均匀增大,检测报警装置非常灵敏且电阻恒定,在一个工作周期内,检测到电路中的电流不是均匀增大时能报警.L是电阻不计的单匝线圈,忽略L的自感,则闭合开关,在一个工作周期内( )| A. | 电压表读数变大 | |
| B. | R0两端电压减小 | |
| C. | 当L近距离扫过某块金属时,金属中产生的电流方向一定不变 | |
| D. | 因为金属中感应电流产生的变化磁场影响了线圈L中的电流,故探测器会报警 |
6.下列论述正确的是( )
| A. | 根据麦克斯韦电磁场理论,变化的磁场一定产生变化的电场. | |
| B. | 光的双缝干涉实验中,若仅将入射光从红光改为紫光,则相邻亮条纹间距一定变大. | |
| C. | 一切物体都在不停地发射红外线,物体温度越高,辐射的红外线越强. | |
| D. | 根据爱因斯坦相对论理论,光源与观察者相互靠近时,观察者观察到的光速比二者相互远离时观察到的光速大. |
10.输出功率恒定的汽车,关于其牵引力与速度的关系,以下说法正确的是( )
| A. | 速度越大牵引力越大 | B. | 速度越大牵引力越小 | ||
| C. | 牵引力与速度无关 | D. | 以上说法都不对 |


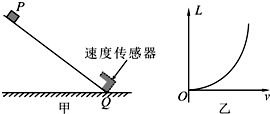 某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:
某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想: