题目内容
2.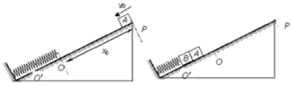 如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0=3$\sqrt{{gx}_{0}sinθ}$顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0块A与斜面间的动摩擦因数为μ=2tanθ,斜面倾角为θ,重力加速度为g求:
如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0=3$\sqrt{{gx}_{0}sinθ}$顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0块A与斜面间的动摩擦因数为μ=2tanθ,斜面倾角为θ,重力加速度为g求:(1)O点和O′点间的距离x1
(2)弹簧在最低点O′处的弹性势能;
(3)在轻弹簧旁边并排放置另一根与之完全相同的弹簧,一端与挡板固定.若将另一个与A材料相同的物块B(可视为质点)与两根弹簧右端拴接,设B的质量为βm将A与B并排在一起,使两根弹簧仍压缩到O′点位置,然后从静止释放,若A离开B后A最终未冲出斜面,求β需满足的条件?
分析 (1)对于物块从P点又回到P点过程,运用动能定理列式,即可求得O点和O′点间的距离x1;
(2)根据能量守恒定律求解弹簧在最低点O′处的弹性势能;
(3)AB刚分离时两者间的弹力为零,根据牛顿第二定律分别求出两者此时的加速度,确定出弹簧此时的状态.再对分离后的过程,由能量守恒列式求解.
解答 解:(1)物块A从P点又回到P点的过程,根据动能定理有:
-2μmgcosθ(x1+x0)=0-$\frac{1}{2}m{v}_{0}^{2}$
又 μ=2tanθ,v0=3$\sqrt{{gx}_{0}sinθ}$
解得:x1=$\frac{1}{8}{x}_{0}$
(2)从O′点到P点,由能量守恒定律得:
弹簧在最低点O′处的弹性势能 EP=μmgcosθ(x1+x0)+mgsinθ(x1+x0)
=$\frac{1}{4}m{v}_{0}^{2}$+mgsinθ•$\frac{{v}_{0}^{2}}{4μgcosθ}$=$\frac{1}{4}m{v}_{0}^{2}$(1+$\frac{tanθ}{μ}$)=$\frac{27}{8}$mgx0sinθ
(3)分离时:aA=aB,NAB=0,
A:aA=gsinθ+μgcosθ
B:2T+βmgsinθ+μβmgcosθ=βmaB
得:T=0,即弹簧处于原长处,A、B两物体分离.
①A、B恰好分离时,分离时A、B速度为零,从O′点到O点有:
2EP=μ(β+1)mgcosθx1+(β+1)mgsinθx1;
得 β=17
②若A恰好回到P点,则有:
2EP=μ(β+1)mgcosθx1+(β+1)mgsinθx1+$\frac{1}{2}$(β+1)mv2;
分离后,A继续上升到静止,有:
$\frac{1}{2}$mv2=(mgsinθ+μmgcosθ)x0;
解得:β=1
综上所述有:1≤β≤17
答:
(1)O点和O′点间的距离x1为$\frac{1}{8}$x0;
(2)弹簧在最低点O′处的弹性势能为$\frac{27}{8}$mgx0sinθ;
(3)β需满足的条件是1≤β≤17.
点评 运用动能定理解题,关键选择合适的研究过程,分析过程中有哪些力做功,确定能量如何转化,然后根据动能定理和能量守恒结合解答.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | 速度的方向就是加速度的方向 | |
| B. | 速度改变量的方向就是加速度的方向 | |
| C. | 速度的方向就是物体运动的方向 | |
| D. | 加速度的方向就是物体运动的方向 |
| A. | 电流将逐渐变大 | |
| B. | 电流将逐渐变小 | |
| C. | 每增加1 V电压而引起的电流变化量是相同的 | |
| D. | 每增加1 V电压而引起的电流变化量是减小的 |
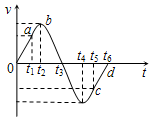 一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )
一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )| A. | t2-t4 | B. | t1-t4 | C. | t1-t5 | D. | t2-t3 |
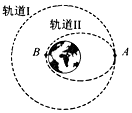 如图,航天飞机在完成太空任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的近地点,关于航天飞机的运动,下列说法中正确的有( )
如图,航天飞机在完成太空任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的近地点,关于航天飞机的运动,下列说法中正确的有( )| A. | 在轨道Ⅱ上经过A的速度小于经过B的速度 | |
| B. | 在轨道Ⅱ上经过A的速度等于在轨道Ⅰ上经过A的速度 | |
| C. | 在轨道Ⅱ上运动的周期等于在轨道Ⅰ上运动的周期 | |
| D. | 在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度 |
 如图,光滑水平面上放一质量M=3kg,长为L=1m的木板,板上最右端放一质量为m=1kg的小物块,接触面间的动摩擦因数为u=0.1,今对木板施加一水平向右的拉力F.
如图,光滑水平面上放一质量M=3kg,长为L=1m的木板,板上最右端放一质量为m=1kg的小物块,接触面间的动摩擦因数为u=0.1,今对木板施加一水平向右的拉力F. 一个滑雪者从静止开始沿山坡滑下,如图所示.山坡的倾角θ=30°,滑雪板与雪地的动摩擦因数是$\frac{1}{5\sqrt{3}}$ (g取10m/s2)
一个滑雪者从静止开始沿山坡滑下,如图所示.山坡的倾角θ=30°,滑雪板与雪地的动摩擦因数是$\frac{1}{5\sqrt{3}}$ (g取10m/s2)