题目内容
11. 如图,光滑水平面上放一质量M=3kg,长为L=1m的木板,板上最右端放一质量为m=1kg的小物块,接触面间的动摩擦因数为u=0.1,今对木板施加一水平向右的拉力F.
如图,光滑水平面上放一质量M=3kg,长为L=1m的木板,板上最右端放一质量为m=1kg的小物块,接触面间的动摩擦因数为u=0.1,今对木板施加一水平向右的拉力F.(1)要使木板能从物块下面抽出来,作用在木板上至少需要用多大的力?
(2)如果拉力F=10N,且恒定不变,则:小物块所能获得的最大速率是多少?
(3)若水平向右的力施加在物块上,要使物块能从木板上面拉出来,F至少需要多大?
分析 (1)要使木板能从物块下面抽出来,小物块相对于木板滑动,隔离对小物块分析,求出它的临界加速度,再对整体分析,运用牛顿第二定律求出拉力的最小值;
(2)当拉力F大于4N时,二者相对滑动,分别对两物体受力分析,由牛顿第二定律求得加速度;再由位移公式及位移关系可求得离开时间,最后根据速度时间公式求出小物块的速度;
(3)当小物块与长木板刚好要发生相对滑动时,作用在小木块上的力最小,根据牛顿第二定律,运用整体法和隔离法列方程求出最小拉力.
解答 解:(1)当小物块与长木板刚好要发生相对滑动时,作用在木板上的力最小,
对小物块,由牛顿第二定律得,μmg=ma,
解得:a=μg=0.1×10m/s2=1m/s2,
对整体,由牛顿第二定律得,
Fmin=(M+m)a=(3+1)×1N=4N.
(2)当F=10N>4N时,两者发生相对滑动,
对小物体:a1=a=1m/s2,
对木板:F-μmg=Ma2,
代入数据解得:a2=3m/s2,
由位移关系有:L=$\frac{1}{2}$a2t2-$\frac{1}{2}$a1t2 ,
代入数据解得:t=2 s,
则小物块的速度为:v1=a1t=2 m/s.
(3)当小物块与长木板刚好要发生相对滑动时,作用在小木块上的力最小,
对于小木块,由牛顿第二定律得,F′-μmg=ma′…①
对整体,由牛顿第二定律得,F′=(M+m)a′…②
联立①②代入数据可解得:F′=$\frac{4}{3}$N.
答:(1)作用在木板上至少需要用4N的力;
(2)小物块所能获得的最大速率是2 m/s;
(3)要使物块能从木板上面拉出来,F至少需要$\frac{4}{3}$N.
点评 解决本题的关键理清物块和木板在整个过程中的运动规律,结合牛顿第二定律和运动学公式,抓住位移关系即可正确解题,有一定的难度.

 一台理想变压器的原、副线圈的匝数比是5:1,原线圈接入电压为220V的正弦交流电,各元件正常工作,一只理想二极管和一个滑动变阻器R串联接在副线圈上,如图所示,电压表和电流表均为理想交流电表.则下列说法正确的是( )
一台理想变压器的原、副线圈的匝数比是5:1,原线圈接入电压为220V的正弦交流电,各元件正常工作,一只理想二极管和一个滑动变阻器R串联接在副线圈上,如图所示,电压表和电流表均为理想交流电表.则下列说法正确的是( )| A. | 原、副线圈中的电流之比为5:1 | |
| B. | 电压表的读数约为44V | |
| C. | 若滑动变阻器接入电路的阻值为20Ω,则1 分钟内产生的热量为2904 J | |
| D. | 若将滑动变阻器的滑片向上滑动,则两电表读数均增大 |
| A. | 质子 | B. | 氘核 | C. | α粒子 | D. | 钠离子 |
| A. | 气体的内能是分子热运动的动能和分子间的势能之和 | |
| B. | 将一个分子从无穷远处靠近另一个分子,则分子力先增大后减小最后再增大 | |
| C. | 功可以全部转化为热,但热量不能全部转化为功 | |
| D. | 热量能够自发地从高温物体传递到低温物体,但不能自发地从低温物体传递到高温物体 | |
| E. | 一定量的气体,分子每秒平均碰撞次数随着温度降低而减小 |
| A. | 4 m | B. | 6 m | C. | 8m | D. | 12 m | ||||
| E. | 15m |
| A. | 100m | B. | 125m | C. | 200m | D. | 80m |

| A. | a、b两处的磁感应强度大小Ba<Bb | |
| B. | a、b两处的磁感应强度大小Ba>Bb | |
| C. | 两条磁感线的空隙处不存在磁场 | |
| D. | 磁感线上某点的切线方向就是该点的磁场方向 |
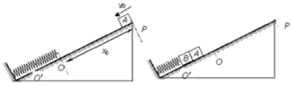 如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0=3$\sqrt{{gx}_{0}sinθ}$顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0块A与斜面间的动摩擦因数为μ=2tanθ,斜面倾角为θ,重力加速度为g求:
如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0=3$\sqrt{{gx}_{0}sinθ}$顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0块A与斜面间的动摩擦因数为μ=2tanθ,斜面倾角为θ,重力加速度为g求: