题目内容
19．
如图所示，两轻弹簧a，b悬挂一小铁球处于平衡状态，弹簧a与竖直方向成30°，弹簧b水平，则剪断弹簧b瞬间小球的加速度大小为（ ）| A． | $\frac{\sqrt{3}}{3}$g | B． | $\frac{2\sqrt{3}}{3}$g | C． | $\frac{\sqrt{3}}{2}$g | D． | g |
分析 先研究剪断弹簧b前小球的受力情况，受到重力和两个弹簧的弹力，根据平衡条件并运用合成法得到两个弹力的大小，再研究剪断弹簧b瞬间小球的受力，抓住a弹簧的弹力不变，由牛顿第二定律求小球的加速度大小．
解答 解：剪断弹簧b前，对小球受力分析，受到重力和两个弹簧的弹力，如图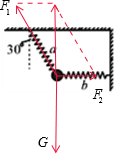
．
根据平衡条件，弹簧b的弹力为：F2=Gsin30°=mgtan30°
剪断弹簧b瞬间弹簧a的弹力不变，小球的重力不变，则小球的合力与弹簧b原来的弹力大小相等、方向相反，所以此瞬间小球的合力大小等于：
F2=Gsin30°=mgtan30°
根据牛顿第二定律得：mgtan30°=ma
解得：a=$\frac{\sqrt{3}}{3}$g
故选：A
点评 本题的关键要抓住弹簧的弹力不能突变，要知道三个共点力平衡时，任意两个力的合力一定与第三个力等值、反向、共线．
练习册系列答案
相关题目
9．a、b两球处在离地高度相同的同一水平面上，a球由静止释放，b球同时以初速度v0水平抛出，忽略空气阻力，则下列说法正确的是（ ）
| A． | b球先落地 | |
| B． | a、b两球均做匀变速运动 | |
| C． | a、b两球落地前的瞬间速率相同 | |
| D． | a、b两球落地前的瞬间速度方向相同 |
10．
2016年10月19日凌晨，“天宫二号”和“神舟十一号”在离地高度为393公里的太空相约，两个比子弹速度还要快8倍的空中飞行器安全无误差地对接在一起，假设“天宫二号”与“神舟十一号”对接后绕地球做匀速圆周运动，己知同步轨道离地高度约为36000公里，则下列说法正确的是（ ）
2016年10月19日凌晨，“天宫二号”和“神舟十一号”在离地高度为393公里的太空相约，两个比子弹速度还要快8倍的空中飞行器安全无误差地对接在一起，假设“天宫二号”与“神舟十一号”对接后绕地球做匀速圆周运动，己知同步轨道离地高度约为36000公里，则下列说法正确的是（ ）| A． | 为实现对接，“神舟十一号”应在离地高度低于393公里的轨道上加速，逐渐靠近“天宫二号” | |
| B． | “比子弹快8倍的速度”大于7.9×103m/s | |
| C． | 对接后运行的周期小于24h | |
| D． | 对接后运行的加速度因质量变大而变小 |
14．
如图所示，某人身系弹性绳自高空P点自由下落，a点是弹性绳的原长位置，b点是人静止悬挂时的平衡位置，c点是人所能到达的最低点，若把P点到a点的过程称为过程I，由a点到c点的过程称为过程II，不计空气阻力，下列说法正确的是（ ）
如图所示，某人身系弹性绳自高空P点自由下落，a点是弹性绳的原长位置，b点是人静止悬挂时的平衡位置，c点是人所能到达的最低点，若把P点到a点的过程称为过程I，由a点到c点的过程称为过程II，不计空气阻力，下列说法正确的是（ ）| A． | 过程II中人的机械能守恒 | |
| B． | 过程II中人的动量的改变量大小等于过程I中重力的冲量大小 | |
| C． | 过程II中人的动能逐渐减小到零 | |
| D． | 过程I中人的动量的改变量等于重力的冲量 |
11．汽车在一条平直公路上，若从静止启动到最大速度的时间内做匀加速直线运动，则汽车做匀加速直线运动的加速度大小为（ ）
| 起动的快慢/s （0～30m/s的加速时间） | 最大速度/m•s-1 |
| 12 | 50 |
| A． | 2.5m/s | B． | 5m/s | C． | 4.17m/s | D． | 9m/s |
如图所示，风洞实验室中可产生水平方向的、大小可调解的风力．现将一套有小球的细直杆放入风洞实验室，小球直径略大于杆直径．已知小球质量为1kg
如图所示，水平面OC上有一质量M=3Kg的静止滑板，滑板高度h=0.8m，与水平面OB间的动摩擦因数μ1=0.1，水平面A处设置一固定的障碍物（摩擦可忽略）．现有一质量为m=5kg的物块（可看成质点），以初速度V0=8m/s滑上滑板左端，物块与滑板间的动摩擦因数μ2=0.4，滑板在碰到障碍物时恰好与物块达到共同速度．当滑板撞到障碍物立即会粘住不动，而物块被抛出后，落在水平面上B点时速度与水平地面的夹角为53°，已知sin53°=0.8，cos53°=0.6，g=10m/s2，求：