题目内容
4.一木块静止在粗糙水平面上,现用一大小为F1的水平力拉动木块,经过时间t,其速度为υ.若将水平拉力的大小改为F2,物体从静止开始经过相等时间t,速度变为2υ.对以上两个过程,用WF1、WF2分别表示拉力F1、F2做的功,Wf1、Wf2分别表示前后两次克服摩擦力做的功,则( )| A. | WF2>4WF1 Wf2>2 Wf1 | B. | WF2>4WF1 Wf2=2 Wf1 | ||
| C. | WF2<4WF1 Wf2=2 Wf1 | D. | WF2<4WF1 Wf2 <2 Wf1 |
分析 根据匀变速直线运动的位移等于平均速度乘以时间,求出位移之比,两次物体所受的摩擦力不变,根据W=fs求解克服摩擦力做功之比,对两个过程,分别根据动能定理列式,联立方程即可求解F1,F2所做的功的关系.
解答 解:由题意可知,两次物体均做匀加速运动,在同样的时间内,它们的位移之比为:
S1:S2=$\frac{v}{2}$t:$\frac{2v}{2}t$=1:2;
两次物体所受的摩擦力不变,根据力做功表达式,则克服滑动摩擦力做功之比为:
Wt1:Wt2=fS1:fS2=1:2,
则有:Wf2=2 Wf1.
再由动能定理,则有:
WF-Wf=$\frac{1}{2}$mv2-0;
可知:WF1-Wf1=$\frac{1}{2}$mv2-0;WF2-Wf2=$\frac{1}{2}$m(2v)2-0;
由上两式可解得:WF2=4WF1-2Wf1,则有:WF2<4WF1 ,故C正确,ABD错误;
故选:C
点评 本题主要考查了恒力做功公式及动能定理的直接应用,解答时要注意两次拉动的过程中,滑动摩擦力是不变的,求出位移关系即可求出摩擦力做功之比.

练习册系列答案
相关题目
14.从地面竖直上抛一物体A,同时在离地面某一高度处有一物体B自由下落,两物体在空中同时到达同一高度时速度大小均为v,则下列说法正确的是( )
| A. | A上抛的初速度与B落地时速度大小相等,都是2v | |
| B. | 两物体在空中运动的时间不相等 | |
| C. | A上升的最大高度与B开始下落时的高度相同 | |
| D. | 两物体在空中同时达到的同一高度处一定是B开始下落时高度的中点 |
12.下列四个物理量的单位中,不属于能量单位的是( )
| A. | 焦耳 | B. | 瓦特 | C. | 千瓦•时 | D. | 伏特•库仑 |
19.如图,一个简单的逻辑电路图.Rl、R2为定值电阻.下列说法正确的是( )
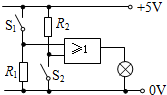

| A. | Sl,S2都断开时灯泡不发光 | B. | Sl,S2都闭合时灯泡发光 | ||
| C. | Sl断开,S2闭合时灯泡发光 | D. | Sl闭合,S2断开时灯泡不发光 |
14. 如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )
如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )
 如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )
如图所示是某卫星绕地球飞行的三条轨道,其中轨道1是近地圆形轨道,轨道2和3是变轨后的椭圆轨道,它们相切于A点.卫星在轨道1上运行时经过A点的速率为v,加速度大小为a,下列说法正确的是( )| A. | 卫星在轨道2上经过A点时的速率大于v | |
| B. | 卫星在轨道2上经过A点时的加速度大于a | |
| C. | 卫星在轨道2上运行的周期大于在轨道3上运行的周期 | |
| D. | 卫星在轨道2上具有的机械能大于在轨道3上具有的机械能 |
 如图,长为L的轻杆一端固定在光滑铰链上,另一端固定一质量为m的小球.一水平向右的拉力作用于杆的中点,使杆以角速度ω匀速转动,当杆与竖直方向成θ角时,拉力F=2mgtgθ,此时拉力F的功率P=mgLωsinθ.(重力加速度为g)
如图,长为L的轻杆一端固定在光滑铰链上,另一端固定一质量为m的小球.一水平向右的拉力作用于杆的中点,使杆以角速度ω匀速转动,当杆与竖直方向成θ角时,拉力F=2mgtgθ,此时拉力F的功率P=mgLωsinθ.(重力加速度为g) 如图,质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强E=$\frac{mg}{3q}$.开始时,杆OB与竖直方向的夹角θ=60°.
如图,质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强E=$\frac{mg}{3q}$.开始时,杆OB与竖直方向的夹角θ=60°. 某兴趣小组利用如图a所示实验装置测重力加速度.倾斜的球槽中放有若干个小铁球,闭合开关K,电磁铁吸住第1个小球.手动敲击弹性金属片M,M与触头瞬间分开,第1个小球开始下落,M迅速恢复,电磁铁又吸住第2个小球.当第1个小球撞击M 时,M与触头分开,第2个小球开始下落….这样,就可测出n个小球下落的总时间T.
某兴趣小组利用如图a所示实验装置测重力加速度.倾斜的球槽中放有若干个小铁球,闭合开关K,电磁铁吸住第1个小球.手动敲击弹性金属片M,M与触头瞬间分开,第1个小球开始下落,M迅速恢复,电磁铁又吸住第2个小球.当第1个小球撞击M 时,M与触头分开,第2个小球开始下落….这样,就可测出n个小球下落的总时间T.