题目内容
6. (1)某人用多用电表按正确步骤测量一电阻阻值.指针指示位置如图所示.则这电阻阻值是1200Ω.如果要用这多用表测量一个约200Ω的电阻,为了测量比较准确,选择开关应选欧姆档的×10.
(1)某人用多用电表按正确步骤测量一电阻阻值.指针指示位置如图所示.则这电阻阻值是1200Ω.如果要用这多用表测量一个约200Ω的电阻,为了测量比较准确,选择开关应选欧姆档的×10.(2)某位同学用多用电表测量一个定值电阻的阻值.多用电表的欧姆挡有R×1、R×10、R×100三挡.他用R×10挡测量电阻时,发现电表的指针偏转角度很大,于是他进行了如下的操作,完成了实验.
A.将电表选择开关旋到R×100挡
B.用电表的两个表笔接触电阻的两端,进行正确的读数
C.将测量的结果记录下来
请指出该同学测量步骤中的错误和遗漏之处应将开关旋至×1档;重新进行欧姆调零.
分析 欧姆表刻度不均匀,为了读数准确应尽量使指针在中间刻度附近;
同时明确零刻度在最右边,偏角小说明阻值大,要准确测量,应换较大挡使指针指在中央附近.每次换挡后都要重新进行欧姆调零.
解答 解:(1)由图可知,采用欧姆档×100档位,则读数为12×100=1200Ω,若测量约200Ω的电阻,为了让指针指在中间刻度附近,故应采用×10档位;
(2)他用R×10挡测量电阻时,发现电表的指针偏角很大,知电阻较小,则换用R×1挡,换挡后需重新欧姆调零,所以操作中遗漏之处为重新欧姆调零.
故答案为:(1)1200;×10;(2)应将开关旋至×1档;重新进行欧姆调零
点评 本题考查了欧姆表的表盘刻度特点,一定要注意每次换挡后都要重新进行欧姆调零.

练习册系列答案
相关题目
17.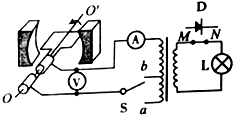 如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )
如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )
 如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )
如图所示,一匝数为N=100的矩形线圈,面积S=0.01m2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=2T.线圈通过-理想变压器后,接一标有“6V,3W”字样的灯泡L,变压器原线圈的总匝数为n1=200匝,b是原线圈的中心抽头,副线圈的匝数为n2=20匝.当开关S拨到b位置时,小灯泡恰好正常发光,设小灯泡的电阻不随温度发生变化,则( )| A. | 电路中电压表的读数为30$\sqrt{2}$V | |
| B. | 电路中电流表的读数$\frac{\sqrt{2}}{10}$A | |
| C. | 线圈转动的角速度15$\sqrt{2}$rad/s | |
| D. | 若将开关S拨到a位置.并将一个理想二极管D接到MN之间,其他条件不变,则此时线圈提供的功率为$\frac{3}{4}$W |
14. 电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )
电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )
 电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )
电荷量为+q,质量为m的小球处在竖直向下的匀强磁场中,电场强度大小为E,小球从高为H处静止球从高为H处静止开始释放,设小球在运动过程中始终受到大小恒定的空气阻力Ff的作用,与地面碰撞过程中小球没有能量和电量的损失,重力加速度为g,则( )| A. | 小球与地面第一次碰撞前的速度大小为$\sqrt{\frac{2(mg+qE+{F}_{f})H}{m}}$ | |
| B. | 小球与地面第一次碰撞前的加速度大小为$\frac{mg+qE}{m}$ | |
| C. | 小球从释放到最后静止,运动的总路程为$\frac{(mg+qE+{F}_{f})H}{mg+qE-{F}_{f}}$ | |
| D. | 小球从释放到最后静止,运动的总路程为$\frac{(mg+qE)H}{{F}_{f}}$ |
1.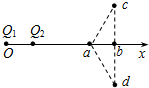 如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )
如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )
 如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )
如图所示,真空中两个不等量的正点电荷Q1、Q2固定在x轴上,其中Q1>Q2.三角形acd为等腰三角形,cd边与x轴垂直且与x轴相交于b点,则下列说法正确的是( )| A. | a点场强小于b点场强 | |
| B. | c点电势等于b点电势 | |
| C. | c点电势等于d点电势 | |
| D. | 将电子从a点移到b点再移到c点电势能增加 |
11.下列说法不正确的是( )
| A. | 互感现象是变压器工作的基础 | |
| B. | 法拉第最先引入“场”的概念,并最早发现了电流的磁效应现象 | |
| C. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看做匀速直线运动,然后把各小段的位移相加,这应用了“微元法” | |
| D. | 伽利略通过实验和论证说明了自由落体运动是一种匀变速直线运动 |
18. 如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )
如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )
 如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )
如图所示,一理想变压器的原、副线圈匝数之比为n1:n2=55:1,原线圈接入电压u=220$\sqrt{2}$sin100πt(V)的交流电源,图中电表均为理想电表,闭合开关后,当滑动变阻器的滑动触头P从最上端滑到最下端的过程中,下列说法正确的是( )| A. | 副线圈中交变电流的频率为100Hz | |
| B. | t=0.02s时,电压表的示数为0 | |
| C. | 电流表的示数先变小后变大 | |
| D. | 定值电阻R消耗的功率先变大后变小 |
3. 如图所示,空间有与水平方向成θ角的匀强电场,一个质量为m的带电小球,用长为L的绝缘细线悬挂于O点.当小球静止时,细线恰好处于水平位置.现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变,则该外力做的功为( )
如图所示,空间有与水平方向成θ角的匀强电场,一个质量为m的带电小球,用长为L的绝缘细线悬挂于O点.当小球静止时,细线恰好处于水平位置.现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变,则该外力做的功为( )
 如图所示,空间有与水平方向成θ角的匀强电场,一个质量为m的带电小球,用长为L的绝缘细线悬挂于O点.当小球静止时,细线恰好处于水平位置.现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变,则该外力做的功为( )
如图所示,空间有与水平方向成θ角的匀强电场,一个质量为m的带电小球,用长为L的绝缘细线悬挂于O点.当小球静止时,细线恰好处于水平位置.现用一个外力将小球沿圆弧缓慢地拉到最低点,此过程小球的电荷量不变,则该外力做的功为( )| A. | mgL | B. | mgLtanθ | C. | $\frac{mgL}{tanθ}$ | D. | $\frac{mgL}{cosθ}$ |

 在研究滑动摩擦力的大小实验探究中,某同学先用弹簧测力计将木块悬挂起来,静止时弹簧测力计示数如图甲所示,然后将木块和木板叠放在水平桌面上,弹簧测力计一端固定,一端与木块水平相连,用力拉动木板,使之在水平面上匀速滑动,如图乙所示,读出测力计的示数为0.6N.则木块和木板间的动摩擦因数为0.2(保留一位有效数字).若用力拉动木板,使之在水平面上加速滑动,其它条件不变,则测力计的示数将等于(填“大于”、“小于”或“等于”)0.6N.
在研究滑动摩擦力的大小实验探究中,某同学先用弹簧测力计将木块悬挂起来,静止时弹簧测力计示数如图甲所示,然后将木块和木板叠放在水平桌面上,弹簧测力计一端固定,一端与木块水平相连,用力拉动木板,使之在水平面上匀速滑动,如图乙所示,读出测力计的示数为0.6N.则木块和木板间的动摩擦因数为0.2(保留一位有效数字).若用力拉动木板,使之在水平面上加速滑动,其它条件不变,则测力计的示数将等于(填“大于”、“小于”或“等于”)0.6N.