题目内容
3.一静止的${\;}_{92}^{232}$U核变为${\;}_{90}^{228}$Th核时放出一个α粒子,已知${\;}_{92}^{232}$U,${\;}_{90}^{228}$Th,α粒子的相对原子质量分别为M0,M1,M2,求放出的α粒子的初动能.分析 根据动量守恒定律和能量守恒列出等式求解问题
解答 解:根据动量守恒定律有
0=M1v1-M2v2
根据能量守恒得:
(M0-M1-M2)C2=$\frac{1}{2}$M1v12+$\frac{1}{2}$M2v22
解以上方程可得:
EKα=$\frac{1}{2}$M2v22=$\frac{{M}_{1}({M}_{0}-{M}_{1}-{M}_{2}){C}^{2}}{{M}_{1}+{M}_{2}}$
答:α粒子的初动能为$\frac{{M}_{1}({M}_{0}-{M}_{1}-{M}_{2}){C}^{2}}{{M}_{1}+{M}_{2}}$
点评 我们要清楚运动过程中能量的转化,以便从能量守恒角度解决问题.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题

练习册系列答案
相关题目
13. 如图所示,游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,他们与盘间的动摩擦因数相同,当圆盘转速缓慢加快到两小孩刚好要发生滑动时,两小孩突然松手,则两小孩的运动情况是( )
如图所示,游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,他们与盘间的动摩擦因数相同,当圆盘转速缓慢加快到两小孩刚好要发生滑动时,两小孩突然松手,则两小孩的运动情况是( )
 如图所示,游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,他们与盘间的动摩擦因数相同,当圆盘转速缓慢加快到两小孩刚好要发生滑动时,两小孩突然松手,则两小孩的运动情况是( )
如图所示,游乐场有一水上转台,可在水平面内匀速转动,沿半径方向面对面手拉手坐着甲、乙两个小孩,他们与盘间的动摩擦因数相同,当圆盘转速缓慢加快到两小孩刚好要发生滑动时,两小孩突然松手,则两小孩的运动情况是( )| A. | 两小孩均沿半径方向滑出后落入水中 | |
| B. | 两小孩仍随圆盘一起做匀速圆周运动,不会发生滑动而落入水中 | |
| C. | 甲仍随圆盘一起做匀速圆周运动,乙发生滑动最终落入水中 | |
| D. | 不知道甲乙质量关系,所以运动情况无法确定 |
18. 如图所示的竖直平面内,水平条形区域I和Ⅱ内有方向垂直竖直面向里的匀强磁场,其宽度均为d,I和Ⅱ之间有一宽度为h的无磁场区域,h>d.一质量为m、边长为d的正方形线框由距区域I上边界某一高度处静止释放,在穿过两磁场区域的过程中,通过线框的电流及其变化情况相同.重力加速度为g,空气阻力忽略不计.则下列说法正确的是( )
如图所示的竖直平面内,水平条形区域I和Ⅱ内有方向垂直竖直面向里的匀强磁场,其宽度均为d,I和Ⅱ之间有一宽度为h的无磁场区域,h>d.一质量为m、边长为d的正方形线框由距区域I上边界某一高度处静止释放,在穿过两磁场区域的过程中,通过线框的电流及其变化情况相同.重力加速度为g,空气阻力忽略不计.则下列说法正确的是( )
 如图所示的竖直平面内,水平条形区域I和Ⅱ内有方向垂直竖直面向里的匀强磁场,其宽度均为d,I和Ⅱ之间有一宽度为h的无磁场区域,h>d.一质量为m、边长为d的正方形线框由距区域I上边界某一高度处静止释放,在穿过两磁场区域的过程中,通过线框的电流及其变化情况相同.重力加速度为g,空气阻力忽略不计.则下列说法正确的是( )
如图所示的竖直平面内,水平条形区域I和Ⅱ内有方向垂直竖直面向里的匀强磁场,其宽度均为d,I和Ⅱ之间有一宽度为h的无磁场区域,h>d.一质量为m、边长为d的正方形线框由距区域I上边界某一高度处静止释放,在穿过两磁场区域的过程中,通过线框的电流及其变化情况相同.重力加速度为g,空气阻力忽略不计.则下列说法正确的是( )| A. | 线框进入区域Ⅰ时与离开区域Ⅰ时的电流方向相同 | |
| B. | 线框进入区域Ⅱ时与离开区域Ⅱ时所受安培力的方向相同 | |
| C. | 线框有可能匀速通过磁场区域Ⅰ | |
| D. | 线框通过区域Ⅰ和区域Ⅱ产生的总热量为Q=2mg(d+h) |
11.在“探究功与速度变化的关系”的实验中,计算小车的速度时,应选择纸带上的哪些点进行计算( )
| A. | 小车开始运动的点 | B. | 纸带上远离小车的点 | ||
| C. | 纸带上靠近小车的点 | D. | 确定小车做匀速运动的点 |
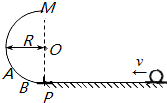 如图所示,竖直平面内有半径为R的半圆形轨道,其直径MP与水平面垂直,在P处另接一水平轨道后,放在水平桌面上,使质量为m的小球在水平轨道上以一定的速度启动.若轨道无摩擦,小球恰好能滚过M点;若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,求在第二种情况中,小球在运动到A点的过程中,克服摩擦阻力所做的功.
如图所示,竖直平面内有半径为R的半圆形轨道,其直径MP与水平面垂直,在P处另接一水平轨道后,放在水平桌面上,使质量为m的小球在水平轨道上以一定的速度启动.若轨道无摩擦,小球恰好能滚过M点;若轨道在B点以下是有摩擦的,那么小球只能滚到图中的A点,OA与OP夹角为60°,求在第二种情况中,小球在运动到A点的过程中,克服摩擦阻力所做的功. 如图所示,质量分别为m和2m的两个小物体可视为质点,用轻质细绳连接,跨过光滑半圆柱体,轻的与桌面接触,重的恰好与圆心一样高,若无初速地释放,则物体m上升到圆弧最高点时小球的速度是多少?(物体大小忽略不计)
如图所示,质量分别为m和2m的两个小物体可视为质点,用轻质细绳连接,跨过光滑半圆柱体,轻的与桌面接触,重的恰好与圆心一样高,若无初速地释放,则物体m上升到圆弧最高点时小球的速度是多少?(物体大小忽略不计) 有一个单摆,当做小角度(θ<5°)摆动时,摆球的振动图象如图所示,求摆球摆到最低点时的速度为0.45m/s.
有一个单摆,当做小角度(θ<5°)摆动时,摆球的振动图象如图所示,求摆球摆到最低点时的速度为0.45m/s. 如图所示,一根张紧的水平弹性长绳上的a、b两点,相距4.5m,a点在b点的左方.当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移恰好为零,且向下运动;此后再经过t=3.0s,a点恰好第二次通过平衡位置,设该波的波长2m≤λ≤3m.求
如图所示,一根张紧的水平弹性长绳上的a、b两点,相距4.5m,a点在b点的左方.当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移恰好为零,且向下运动;此后再经过t=3.0s,a点恰好第二次通过平衡位置,设该波的波长2m≤λ≤3m.求