题目内容
14. 如图所示,固定的竖直光滑圆孤轨道的半径R=1.25m,A点与圆心O在同一水平线上,圆孤轨道底端B点与圆心在同一竖直线上,水平传送带以v0=4.0m/s的速度逆时针匀速运转,质量为0.5kg的物块从轨道上的A点由静止释放.已知传送带长度为L=3.0m,物块与传送带间的动摩擦因数μ=0.5,不计物块通过轨道与传送带交接处的动能损失,取g=10m/s2,试求:
如图所示,固定的竖直光滑圆孤轨道的半径R=1.25m,A点与圆心O在同一水平线上,圆孤轨道底端B点与圆心在同一竖直线上,水平传送带以v0=4.0m/s的速度逆时针匀速运转,质量为0.5kg的物块从轨道上的A点由静止释放.已知传送带长度为L=3.0m,物块与传送带间的动摩擦因数μ=0.5,不计物块通过轨道与传送带交接处的动能损失,取g=10m/s2,试求:(1)物块从A点下滑到B点时受到轨道的支持力大小FN;
(2)物块在传送带上向右运动,到达最右端时到B点的距离x:
(3)若物块每次到达传送带上最右端时,电动机驱动传送带的速度立即减小△v=1.0m/s,物块最终停止时,在传送带上相对于地面运动的总路程S.
分析 (1)物块从A滑到B的过程中,由动能定理求出物块滑到B点时的速度,由牛顿第二定律求解物块受到轨道的支持力大小FN;
(2)分析物块传动带带后的运动过程:物块滑上传送带后做匀减速直线运动,速度减至零时到达最右端,由牛顿第二定律和运动学公式结合求解;
(3)物块每次到达传送带上最右端时,电动机驱动传送带的速度立即减小,物块向左加速,滑上圆弧后又滑下,再次滑上传送带,分析出物块的运动规律,结合运动学公式求出总路程.
解答 解:(1)根据动能定理得,mgR=$\frac{1}{2}m{v}^{2}$,
解得物块到达B点的速度v=$\sqrt{2gR}=\sqrt{2×10×1.25}$m/s=5m/s,
根据牛顿第二定律得,${F}_{N}-mg=m\frac{{v}^{2}}{R}$,解得${F}_{N}=mg+m\frac{{v}^{2}}{R}=5+0.5×\frac{25}{1.25}N$=15N.
(2)物块滑上传送带后,向右做匀减速直线运动,则到达最右端时到B点的距离x=$\frac{{v}^{2}}{2a}=\frac{{v}^{2}}{2μg}=\frac{25}{2×0.5×10}m=2.5m$.
(3)物块第一次滑动最右端再回到B点相对地面运动的路程s1=2x=2×2.5m=5m,
第一次返回到B点的速度v1=v0-△v=3m/s,则物块第二次向右匀减速直线运动的位移${x}_{1}=\frac{{{v}_{1}}^{2}}{2a}=\frac{9}{10}m=0.9m$,
物块第二次滑到最右端再回到B点相对地面运动的路程s2=2x1=2×0.9m=1.8m,
第二次返回到B点的速度v2=v1-△v=3-1m/s=2m/s,则物块第三次向右匀减速直线运动的位移${x}_{2}=\frac{{{v}_{2}}^{2}}{2a}=\frac{4}{10}m=0.4m$,
物块第三次滑到最右端再回到B点相对地面的路程s3=2x2=2×0.4m=0.8m,
第三次返回到B点的速度v3=v2-△v=2-1m/s=1m/s,则物块第四次向右匀减速直线运动的位移${x}_{3}=\frac{{{v}_{3}}^{2}}{2a}=\frac{1}{10}m=0.1m$,
因为物块到达最右端时,速度立即减小1m/s,则物块第四次到达最右端后,传送带速度为零,物块静止.
则总路程S=s1+s2+s3+x3=5+1.8+0.8+0.1m=7.7m.
答:(1)物块从A点下滑到B点时受到轨道的支持力大小为15N;
(2)物块在传送带上向右运动,到达最右端时到B点的距离x为2.5m;
(3)物块最终停止时,在传送带上相对于地面运动的总路程为7.7m.
点评 本题考查了动能定理、牛顿第二定律和运动学公式的综合运用,对于第三问,关键理清物块在整个过程中的运动规律,确定出物块最终停在的位置,结合运动学公式灵活求解.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | 电压表 | B. | 电流表 | C. | 滑动变阻器 | D. | 秒表 |
| A. | 物块水平抛出时的动能与重力势能相等 | |
| B. | 落地时的重力功率是水平抛出时重力功率的两倍 | |
| C. | 落地时的速度大小为水平初速度大小的两倍 | |
| D. | 重力做功的大小是水平抛出时物块动能的两倍. |
 洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )
洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
 如图所示,斜面体的质量为M、斜角为θ,放置在水平面上,各接触面为粗糙.
如图所示,斜面体的质量为M、斜角为θ,放置在水平面上,各接触面为粗糙.
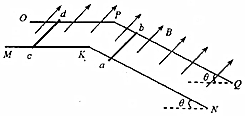 如图所示,足够长、倾角θ=37°的光滑倾斜导轨与粗糙水平导轨相连,导轨宽L=1m,处在垂直于倾斜导轨向上的匀强磁场B中;导体棒ab和cd都垂直于导轨,ab在倾斜导轨上,cd在水平导轨上,质量都是m=0.2kg,电阻分别为rab=2Ω,rcd=3Ω.ab棒由静止开始运动,经过一段时间,通过cd棒电荷量q=1C,ab刚好达到最大速度v=6m/s,cd始终静止.sin37°=0.6,cos37°=0.8,g=10m/s2.导轨电阻不计.求:
如图所示,足够长、倾角θ=37°的光滑倾斜导轨与粗糙水平导轨相连,导轨宽L=1m,处在垂直于倾斜导轨向上的匀强磁场B中;导体棒ab和cd都垂直于导轨,ab在倾斜导轨上,cd在水平导轨上,质量都是m=0.2kg,电阻分别为rab=2Ω,rcd=3Ω.ab棒由静止开始运动,经过一段时间,通过cd棒电荷量q=1C,ab刚好达到最大速度v=6m/s,cd始终静止.sin37°=0.6,cos37°=0.8,g=10m/s2.导轨电阻不计.求: