题目内容
10.如图所示,各边长均为l的塔形金属线框(对边为5l)放置于水平面上,在其右侧有与其形状、大小完全相同的磁场区域,磁场方向竖直向上,现使线框在外力F的作用下向右做匀速直线运动,取电流顺时针方向为正,如果从线框进入磁场开始计时,则下列能正确描述线框中电流随线框向右移动距离的变化关系图象是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
分析 根据切割的有效长度,根据E=BLV和欧姆定律得出感应电流,通过右手定则判断感应电流的方向,从而确定正确的图线.
解答 解:金属线框向右匀速运动的过程中,从进入磁场开始,0-2l内,切割的有效长度为l,电流I=$\frac{Blv}{R}$,根据右手定则知,方向为顺时针方向.
2l-4l内,切割的有效长度为2l,电流I=$\frac{2Blv}{R}$,根据右手定则知,方向为顺时针方向.
4l-5l内,切割的有效长度为3l,电流I=$\frac{3Blv}{R}$,根据右手定则知,方向为顺时针方向.
5l-6l内,切割的有效长度为3l,电流I=$\frac{3Blv}{R}$,根据右手定则知,方向为逆时针方向.
6l-8l内,切割的有效长度为2l,电流I=$\frac{2Blv}{R}$,根据右手定则知,方向为逆时针方向.
8l-10l内,切割的有效长度为l,电流I=$\frac{Blv}{R}$,根据右手定则知,方向为逆时针方向.故D正确,A、B、C错误.
故选:D.
点评 解决本题的关键要理清线框在运动过程中有效长度的变化,掌握切割产生的感应电动势公式,会运用右手定则或楞次定律判断感应电流的方向.

练习册系列答案
相关题目
1. 如图所示,地面上方有一宽度为L的矩形磁场区域,区域内存在着水平方向(垂直于纸面向里)的匀强磁场,磁感应强度为B.质量为m的单匝正方形闭合金属线框电阻为R,边长为L.现将线框从距磁场上界面高h处由静止释放,线框进入磁场后落到地面上,线框在运动过程中始终保持在竖直平面内,且不发生转动,空气阻力不计,重力加速度为g.若多次改变h使其由0逐渐增大,则下列说法正确的是( )
如图所示,地面上方有一宽度为L的矩形磁场区域,区域内存在着水平方向(垂直于纸面向里)的匀强磁场,磁感应强度为B.质量为m的单匝正方形闭合金属线框电阻为R,边长为L.现将线框从距磁场上界面高h处由静止释放,线框进入磁场后落到地面上,线框在运动过程中始终保持在竖直平面内,且不发生转动,空气阻力不计,重力加速度为g.若多次改变h使其由0逐渐增大,则下列说法正确的是( )
 如图所示,地面上方有一宽度为L的矩形磁场区域,区域内存在着水平方向(垂直于纸面向里)的匀强磁场,磁感应强度为B.质量为m的单匝正方形闭合金属线框电阻为R,边长为L.现将线框从距磁场上界面高h处由静止释放,线框进入磁场后落到地面上,线框在运动过程中始终保持在竖直平面内,且不发生转动,空气阻力不计,重力加速度为g.若多次改变h使其由0逐渐增大,则下列说法正确的是( )
如图所示,地面上方有一宽度为L的矩形磁场区域,区域内存在着水平方向(垂直于纸面向里)的匀强磁场,磁感应强度为B.质量为m的单匝正方形闭合金属线框电阻为R,边长为L.现将线框从距磁场上界面高h处由静止释放,线框进入磁场后落到地面上,线框在运动过程中始终保持在竖直平面内,且不发生转动,空气阻力不计,重力加速度为g.若多次改变h使其由0逐渐增大,则下列说法正确的是( )| A. | 线框落地前的速度将一直增大 | |
| B. | 线框进入磁场时的加速度的值可能大于g | |
| C. | 线框落地时重力的功率一定是$\frac{{m}^{2}{g}^{2}R}{{B}^{2}{L}^{2}}$ | |
| D. | 通过线框横截面的电荷量一定是$\frac{B{L}^{2}}{R}$ |
18. 如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
 如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )
如图所示,水平轨道宽为L,轨道区间里存在着斜向上与水平方向夹角为α的匀强磁场.一质量为m的导体棒垂直导轨放置,与导轨右端的距离为s,导体棒与导轨间动摩檫因数为μ.某时刻起给导体棒通以如图所示的恒定电流I,导体棒加速后从轨道右端水平飞出,落在距离水平轨道为h的地面上,落地点与轨道右端的水平距离为s.重力加速度g,忽略空气阻力,则( )| A. | 导体棒刚飞出轨道时的速度大小为s$\sqrt{\frac{g}{h}}$ | |
| B. | 导体棒在空中飞行的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 导体棒在轨道上的加速度大小为$\frac{gs}{4h}$ | |
| D. | 磁感应强度大小为$\frac{mg(s+4μh)}{4hIL(sinα+μcosα)}$ |
19. 如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
 如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )
如图所示,在竖直平面内有一固定的半圆槽,半圆直径AG水平,B、C、D、E、F点将半圆周六等分.现将5个质量不同的小球1、2、3、4、5(均可视为质点)分别从A点开始向右做平抛运动,分别落到B、C、D、E、F点上,则下列说法正确的是( )| A. | 球5到达F点时,速度的反方向延长线必过圆心 | |
| B. | 球3做平抛运动全过程速度变化最大 | |
| C. | 球5做平抛运动的时间最长 | |
| D. | 各球到达圆周时球3的重力功率最大 |
20.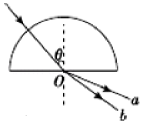 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )| A. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| B. | 在真空中,a光的波长小于b光的波长 | |
| C. | 玻璃砖对a光的折射率小于b光的折射率 | |
| D. | 若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失 | |
| E. | 分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |
 如图所示,质量m=1kg的小球用细线拴住,线长l=1m,细线所受拉力达到F=14N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,重力加速度g=10m/s2,求:
如图所示,质量m=1kg的小球用细线拴住,线长l=1m,细线所受拉力达到F=14N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,重力加速度g=10m/s2,求: 如图所示,两光滑的金属导轨M、N水平放置处在竖直向上的匀强磁场中,搁在导轨上的两金属杆ab和cd垂直于轨,当ab杆沿导轨向右运动时,通过cd杆的电流方向是从d向c,cd杆将向右运动.
如图所示,两光滑的金属导轨M、N水平放置处在竖直向上的匀强磁场中,搁在导轨上的两金属杆ab和cd垂直于轨,当ab杆沿导轨向右运动时,通过cd杆的电流方向是从d向c,cd杆将向右运动. 通过半径相同的两个小球“验证碰撞中的动量守恒”的实验,让质量为m1的小球从斜槽轨道上某处自由滚下,与静止在轨道末端的质量为m2的小球发生对心碰撞(如图所示),则:
通过半径相同的两个小球“验证碰撞中的动量守恒”的实验,让质量为m1的小球从斜槽轨道上某处自由滚下,与静止在轨道末端的质量为m2的小球发生对心碰撞(如图所示),则: