题目内容
6．
如图甲，在倾角为θ=30°的斜面上放一轻质弹簧，其下端固定，静止时上端位置在B点，小物块在A点自由释放，从开始运动的一段时间内的v-t图象如图乙所示，小物块在0.8s时运动到B点，在1.0s时到达C点（图中未标出），在1.3s时到达D点，经过一段时间后回到B点，且速度不为零．取g=10m/s2．由图知（ ）| A． | 小物块从A点运动到D点的过程中，小物块在C点时，弹簧的弹性势能最小 | |
| B． | 小物块从A点运动到D点的过程中，小物块机械能不断减少 | |
| C． | 小物块第一次经过B点的加速度值小于第二次经过B点的加速度值 | |
| D． | 小物块从D点运动到B点的过程中，加速度不断减小 |
分析 弹簧的弹性势能与弹簧的形变量有关，形变量越大，弹性势能越大．除了重力做功以外的力对物体做功将引起物体机械能的变化．由牛顿第二定律分析加速度的变化．
解答 解：A、小物块从A点运动到D点的过程中，弹簧不断被压缩，弹簧的弹性势能逐渐增大，则知小物块在B点时，弹簧的弹性势能最小．故A错误．
B、根据图象的斜率等于加速度，可知物体在AB段运动的加速度为 a=2.5m/s2＜gsin30°，说明物块受到滑动摩擦力作用．
小物块从A点运动到D点的过程中，弹簧的弹力和滑动摩擦力对物块做负功，则小物块机械能不断减少．故B正确．
C、小物块第一次经过B点时，根据牛顿第二定律得：mgsin30°-f=ma1；小物块第二次经过B点时有 mgsin30°+f=ma2；则知小物块第一次经过B点的加速度值小于第二次经过B点的加速度值．故C正确．
D、小物块从D点运动到B点的过程中，由图象的斜率变化知，加速度先减小后反向增大，故D错误．
故选：BC
点评 此题的关键要分析清楚物块运动过程，知道速度时间图象的斜率表示物块的加速度，应用牛顿第二定律、能量守恒定律解决这类问题．
练习册系列答案
优等生题库系列答案
相关题目
16．关于平衡态和热平衡，下列说法中正确的有（ ）
| A． | 只要温度不变且处处相等，系统就一定处于平衡态 | |
| B． | 两个系统在接触时它们的状态不发生变化，这两个系统原来的温度是相等的 | |
| C． | 热平衡就是平衡态 | |
| D． | 处于热平衡的两个系统的温度不一定相等 |
在做平抛实验中，某同学只在竖直板面上记下了重锤线y的方向，但忘记了记下平抛的初位置，在坐标纸上描出了一段曲线的轨迹，如图所示，现在曲线上取A、B两点，量出它们到y轴的距离，AA′=x1，BB′=x2，以及AB的竖直距离h，用这些可以求得小球平抛时初速度为$\sqrt{\frac{（{x}_{2}^{2}-{x}_{1}^{2}）g}{2h}}$．
14．下列说法正确的是（ ）
| A． | 火车转弯时行驶的速度大于规定的安全速度时，轮缘挤压外侧铁轨 | |
| B． | 汽车以相同的速率过桥时，在凸形桥的最高点汽车对桥的压力小于在凹形桥的最低点汽车对桥的压力 | |
| C． | 汽车在坡路转弯时，一定是垂直车身指向内侧的静摩擦力充当向心力 | |
| D． | 汽车在水平路面转弯时，受到了重力、支持力、摩擦力、向心力的作用 |
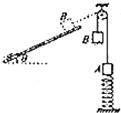如图所示，劲度系数为k的轻弹簧下端周定在水平地面上，上端连接一质量为m的物体A，一不可伸长的轻绳跨过滑轮，两端分别与物体A及质量为2m的物体B连接，不计空气阻力、定滑轮与轻绳间的摩擦，重力加速度为g．弹簧的形变始终在弹性限度内．
2．
如图所示，平行金属板水平正对放置，分别带等量异号电荷．一带电微粒水平射板间，在重力和电场力共作用下运动，轨迹如图中虚线所示，那么（ ）
如图所示，平行金属板水平正对放置，分别带等量异号电荷．一带电微粒水平射板间，在重力和电场力共作用下运动，轨迹如图中虚线所示，那么（ ）| A． | 微粒从M点运动到N点动能一定增加 | |
| B． | 微粒从M点运动到N点电势能一定增加 | |
| C． | 微粒从M点运动到N点机械能一定增加 | |
| D． | 若微粒带正电荷，则A板一定带正电荷 |
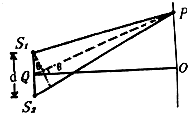如图所示，两个相同的声源S1和S2相距d=10m，频率f=1700Hz，振动为同步振动，Q是S1，S2连线的中点，OQ是S1，S2连线的中垂线，OQ长l=400m，OP线段平行于S1S2连线，OP=16m，已知空气中声速为340m/s，试问：