题目内容
3.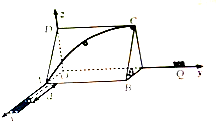 如图,一正方形薄板ABCD的边长为R,薄板上固定一个以正方形的边长为半径的四分之一光滑圆环,薄板靠在与水平地面夹角为θ的墙壁上,建立三维直角坐标系,oz为竖直轴,xOy为水平地面.置于地面上的弹簧枪枪口与AB边的距离为d,弹簧枪发射处的小球沿水平地面上运动一段距离d后,从A处开始沿着圆环内侧冲上薄板,最后从圆环的最高点C水平飞出后落在放置于y轴某处的小桶Q内.已知小球与地面和薄板间的动摩擦因数均为μ,不计小球在拐角A处的机械能损失.求:
如图,一正方形薄板ABCD的边长为R,薄板上固定一个以正方形的边长为半径的四分之一光滑圆环,薄板靠在与水平地面夹角为θ的墙壁上,建立三维直角坐标系,oz为竖直轴,xOy为水平地面.置于地面上的弹簧枪枪口与AB边的距离为d,弹簧枪发射处的小球沿水平地面上运动一段距离d后,从A处开始沿着圆环内侧冲上薄板,最后从圆环的最高点C水平飞出后落在放置于y轴某处的小桶Q内.已知小球与地面和薄板间的动摩擦因数均为μ,不计小球在拐角A处的机械能损失.求:(1)小球能冲上斜面时,其最小发射速度v0
(2)小球能掉入小桶内,小桶Q的坐标值yQ
(3)小球能掉入小桶内,弹簧枪必须具备的最小弹性势能EP.
分析 (1)从小球被从枪口射出到进入斜面,由动能定理可得最小发射速度v0.
(2)小球在轨道上运动的时候,相当于绳模型,由此可得最高点C的最小速度,在C点小球做平抛,结合平抛规律,可以解得小球平抛水平位移,此位移为小桶坐标的最小值.
(3)由小球在C点的最小速度,结合全过程的动能定律和功能关系可得弹簧枪必须具备的最小弹性势能EP.
解答 解:(1)小球刚到斜面速度为零,此时发射速度最小,此过程摩擦力做功,由动能定理可得:
$-μmgd=-\frac{1}{2}m{{v}_{0}}^{2}$,
解得:${v}_{0}=\sqrt{2μgd}$.
(2)小球在斜面轨道上运动时,在C点受力如图:
重力的分力提供向心力的时候,小球向心力为最小值,由此可得:
$mgsinθ=m\frac{{{v}_{C}}^{2}}{R}$,
解得:
${v}_{C}=\sqrt{gRsinθ}$,
C点之后小球做平抛运动,设桶到C的水平距离为X,由平抛规律可得:
$Rsinθ=\frac{1}{2}g{t}^{2}$,
X=vCt,
解得:
$X=\sqrt{2}Rsinθ$,
故可知小球能掉入小桶内,小桶Q的坐标值最小为:
${y}_{Q}=R+X=R+\sqrt{2}Rsinθ$,
故可知小球能掉入小桶内,小桶Q的坐标值为:
${y}_{Q}≥R+\sqrt{2}Rsinθ$.
(3)小球在C点速度最小时,发射时弹簧枪的弹性势能最小,对发射到C整个过程:
${W}_{弹}-mgRsinθ-{W}_{f}=\frac{1}{2}m{{v}_{C}}^{2}$,
弹力做的功等于弹性势能的多少:
W弹=EP,
水平面和斜面摩擦力做功为:
${W}_{f}={f}_{1}{s}_{1}+{f}_{2}{s}_{2}=μmgd+μmgcosθ•\frac{πR}{2}$,
解得:
${E}_{P}=(\frac{3}{2}sinθ+\frac{μπ}{2}cosθ)mgR+μmgd$.
答:(1)小球能冲上斜面时,其最小发射速度$\sqrt{2μgd}$.
(2)小球能掉入小桶内,小桶Q的坐标值${y}_{Q}≥R+\sqrt{2}Rsinθ$.
(3)小球能掉入小桶内,弹簧枪必须具备的最小弹性势能$(\frac{3}{2}sinθ+\frac{μπ}{2}cosθ)mgR+μmgd$.
点评 该题关键是要建立好物理模型,此题突破口在对斜面轨道的处理上,首先要能分析这是个绳模型,会求绳模型最高点的最小速度;其次要有全局观念,弹簧枪必须具备的最小弹性势能,对应C点最小速度.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案| A. | 串联一个570Ω的电阻 | B. | 并联一个570Ω的电阻 | ||
| C. | 串联一个0.05Ω的电阻 | D. | 并联一个0.05Ω的电阻 |
| A. | 核能是一种常规能源 | |
| B. | 煤、石油、天然气都是常规能源 | |
| C. | 大量消耗常规能源加剧了“温室效应” | |
| D. | 燃烧煤炭时产生的二氧化硫使雨水酸度升高,形成酸雨 |
| A. | 物体的动能增加了mgh | B. | 物体的机械能减少了mgh | ||
| C. | 物体克服阻力所做的功为$\frac{1}{5}$mgh | D. | 物体的重力势能减少了mgh |
| A. | 飞机做的是匀速直线运动 | |
| B. | 飞机上的乘客对座椅的压力略大于地球对乘客的引力 | |
| C. | 飞机上的乘客对座椅的压力略小于地球对乘客的引力 | |
| D. | 飞机上的乘客对座椅的压力为零 |
 如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求:
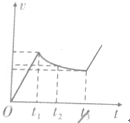
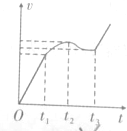
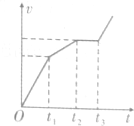
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求: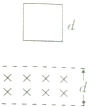 如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
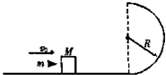 如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以v0=400m/s的水平速度射入木块中,然后一起运动到轨道最高点水平抛出(g取10m/s2),求:
如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以v0=400m/s的水平速度射入木块中,然后一起运动到轨道最高点水平抛出(g取10m/s2),求: