题目内容
15. 如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求:
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求:(1)细线对小球的拉力;
(2)小球圆周运动的向心力;
(3)小球运动的角速度;
(4)当转动加快时,角度θ如何变化.
分析 (1)小球在重力和拉力合力作用下做匀速圆周运动,靠两个力的合力提供向心力,根据牛顿第二定律求出拉力.
(2)由力的合成法求解小球圆周运动的向心力.
(3)由向心力公式F=mrω2求解角速度.
(4)根据离心运动知识分析角度θ的变化.
解答  解:(1)小球受重力和拉力作用,两个力的合力提供向心力,根据合成法得:
解:(1)小球受重力和拉力作用,两个力的合力提供向心力,根据合成法得:
细线对小球的拉力 T=$\frac{mg}{cosθ}$
(2)小球圆周运动的向心力 F=F1=mgtanθ.
(2)根据向心力公式得:F=mrω2,r=Lsinθ
得ω=$\sqrt{\frac{g}{Lcosθ}}$
(4)当转动加快时,球所需要的向心力增大,将做离心运动,所以角度θ增大.
答:
(1)细线对小球的拉力为$\frac{mg}{cosθ}$;
(2)小球圆周运动的向心力为mgtanθ;
(3)小球运动的角速度为$\sqrt{\frac{g}{Lcosθ}}$;
(4)当转动加快时,角度θ增大.
点评 解决本题的关键搞清小球做圆周运动向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5.如图1所示,两个闭合圆形线圈A、B的圆心重合,放在同一水平面内,线圈B中通以如图2所示的交变电流,设t=0时电流沿逆时针方向(图中箭头所示).对于线圈A在t1~t2时间内的下列说法中正确的是( )

| A. | 有顺时针方向的电流,且有扩张的趋势 | |
| B. | 有顺时针方向的电流,且有收缩的趋势 | |
| C. | 有逆时针方向的电流,且有扩张的趋势 | |
| D. | 有逆时针方向的电流,且有收缩的趋势 |
7.下列关于向心加速度的说法中正确的是( )
| A. | 向心加速度的方向始终指向圆心 | |
| B. | 向心加速度的方向保持不变 | |
| C. | 在匀速圆周运动中,向心加速度是恒定的 | |
| D. | 在匀速圆周运动中,向心加速度的大小不断变化 |
2.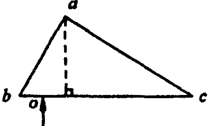 如图为一直角棱镜的横截面,∠bac=90°,∠abc=60°.一平行细光束从O点沿垂直于bc面的方向射入棱镜.已知棱镜材料的折射率n=$\sqrt{2}$,若不考虑原入射光在bc面上的反射光,则有光线( )
如图为一直角棱镜的横截面,∠bac=90°,∠abc=60°.一平行细光束从O点沿垂直于bc面的方向射入棱镜.已知棱镜材料的折射率n=$\sqrt{2}$,若不考虑原入射光在bc面上的反射光,则有光线( )
 如图为一直角棱镜的横截面,∠bac=90°,∠abc=60°.一平行细光束从O点沿垂直于bc面的方向射入棱镜.已知棱镜材料的折射率n=$\sqrt{2}$,若不考虑原入射光在bc面上的反射光,则有光线( )
如图为一直角棱镜的横截面,∠bac=90°,∠abc=60°.一平行细光束从O点沿垂直于bc面的方向射入棱镜.已知棱镜材料的折射率n=$\sqrt{2}$,若不考虑原入射光在bc面上的反射光,则有光线( )| A. | 从ab面射出 | B. | 不能从ac面射出 | ||
| C. | 从bc面射出,且与bc面斜交 | D. | 从bc面射出,且与bc面垂直 |

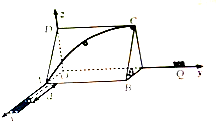 如图,一正方形薄板ABCD的边长为R,薄板上固定一个以正方形的边长为半径的四分之一光滑圆环,薄板靠在与水平地面夹角为θ的墙壁上,建立三维直角坐标系,oz为竖直轴,xOy为水平地面.置于地面上的弹簧枪枪口与AB边的距离为d,弹簧枪发射处的小球沿水平地面上运动一段距离d后,从A处开始沿着圆环内侧冲上薄板,最后从圆环的最高点C水平飞出后落在放置于y轴某处的小桶Q内.已知小球与地面和薄板间的动摩擦因数均为μ,不计小球在拐角A处的机械能损失.求:
如图,一正方形薄板ABCD的边长为R,薄板上固定一个以正方形的边长为半径的四分之一光滑圆环,薄板靠在与水平地面夹角为θ的墙壁上,建立三维直角坐标系,oz为竖直轴,xOy为水平地面.置于地面上的弹簧枪枪口与AB边的距离为d,弹簧枪发射处的小球沿水平地面上运动一段距离d后,从A处开始沿着圆环内侧冲上薄板,最后从圆环的最高点C水平飞出后落在放置于y轴某处的小桶Q内.已知小球与地面和薄板间的动摩擦因数均为μ,不计小球在拐角A处的机械能损失.求: 一根细绳上端固定于O点,下端系一质量为m的小球,线长l,在其中点O′处有一小钉,如图所示,将小球拉至C处,∠AOC=60°,小球从静止释放,摆至最低点A处时小球的速度为$\sqrt{gl}$,当小球摆至右侧最高点B处时,(请在图上画出B点),∠BO′A=90°(不计阻力).
一根细绳上端固定于O点,下端系一质量为m的小球,线长l,在其中点O′处有一小钉,如图所示,将小球拉至C处,∠AOC=60°,小球从静止释放,摆至最低点A处时小球的速度为$\sqrt{gl}$,当小球摆至右侧最高点B处时,(请在图上画出B点),∠BO′A=90°(不计阻力). 用自由落体法验证机械能守恒定律的实验.
用自由落体法验证机械能守恒定律的实验.