题目内容
6. 水平固定的汽缸A和竖直固定的汽缸B内壁光滑长度均为4L、横截面积均为S,A、B之间由一段容积可忽略的带阀门的细管相连,整个装置置于温度27℃、大气压为p0的环境中,活塞C、D的质量及厚度均忽略不计,缸内气体均为理想气体,原长3L、劲度系数k=$\frac{2{p}_{0}S}{L}$的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点,开始时活塞C距汽缸A的底部为1.5L,活塞D距汽缸B的底部为L.求:
水平固定的汽缸A和竖直固定的汽缸B内壁光滑长度均为4L、横截面积均为S,A、B之间由一段容积可忽略的带阀门的细管相连,整个装置置于温度27℃、大气压为p0的环境中,活塞C、D的质量及厚度均忽略不计,缸内气体均为理想气体,原长3L、劲度系数k=$\frac{2{p}_{0}S}{L}$的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点,开始时活塞C距汽缸A的底部为1.5L,活塞D距汽缸B的底部为L.求:①打开阀门,稳定后气缸内温度与环境温度相同,求活塞D上升的距离;
②要想使活塞D回到原来的位置,缸内气体的温度应降到多少度.
分析 ①根据活塞C受力平衡,列出平衡方程求出气缸A内气体的压强为P1,打开活塞后对封闭气体运用玻意耳定律,求出活塞D距汽缸B的底部的高度,再利用几何关系即可求出活塞D上升的距离;
②降温过程压强不变,弹簧的形变量不变,活塞C不动,运用盖吕萨克定律,即可求出缸内气体降到的温度.
解答 解:①设气缸A内气体的压强为P1,
根据平衡对活塞C:p1S=k(1.5L-L)+p0S
解得:p1=2p0
打开阀门后,气缸A内的气体温度保持不变,
根据玻意耳定律可得:p1•1.5LS=p0•x1S
解得活塞D距汽缸B的底部的高度:x1=3L
则D活塞上升距离:△x=3L-L=2L
②活塞D回到原来位置过程中,压强保持不变,
根据盖-吕萨克定律可得:$\frac{4LS}{{T}_{1}}$=$\frac{2LS}{{T}_{2}}$
解得:T2=$\frac{1}{2}$T1=150K=-123℃
答:①活塞D上升的距离为2L;
②要想使活塞D回到原来的位置,缸内气体的温度应降到-123℃.
点评 本题考查玻意耳定律的应用及压强的计算,关键要注意首先明确气体发生的什么变化,根据力平衡法求气体的压强,然后才能分析状态参量,由理想气体的状态方程或实验定律进行分析求解,第二问要注意降温过程压强不变,弹簧的形变量不变,活塞C不动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 甲、乙两船在同一河流中同时开始渡河,河水流速为v0,两船在静水中的速率均为v.甲、乙两船船头均与河岸成θ角,如图所示,已知甲船恰好能垂直到达河正对岸的A点,乙船到达河对岸的B点,A、B之间的距离为L.则下列判断不正确的是( )
甲、乙两船在同一河流中同时开始渡河,河水流速为v0,两船在静水中的速率均为v.甲、乙两船船头均与河岸成θ角,如图所示,已知甲船恰好能垂直到达河正对岸的A点,乙船到达河对岸的B点,A、B之间的距离为L.则下列判断不正确的是( )
 甲、乙两船在同一河流中同时开始渡河,河水流速为v0,两船在静水中的速率均为v.甲、乙两船船头均与河岸成θ角,如图所示,已知甲船恰好能垂直到达河正对岸的A点,乙船到达河对岸的B点,A、B之间的距离为L.则下列判断不正确的是( )
甲、乙两船在同一河流中同时开始渡河,河水流速为v0,两船在静水中的速率均为v.甲、乙两船船头均与河岸成θ角,如图所示,已知甲船恰好能垂直到达河正对岸的A点,乙船到达河对岸的B点,A、B之间的距离为L.则下列判断不正确的是( )| A. | 甲、乙两船同时到达对岸 | |
| B. | 若仅是河水流速v0增大,则两船的渡河时间都不变 | |
| C. | 不论河水流速v0如何改变,只要适当改变θ角,甲船总能到达正对岸的A点 | |
| D. | 若仅是河水流速v0增大,则两船到达对岸时,两船之间的距离仍然为L |
14.下列给出的几种物理情景中,有可能的是( )
| A. | 物体受拉力作用向上匀速运动,拉力做的功是1J,但物体重力势能的增加量不是1J | |
| B. | 物体受拉力作用向上运动,拉力做的功是1J,但物体重力势能的增加量不是1J | |
| C. | 没有摩擦时物体由A沿直线运动到B,克服重力做的功是1 J,有摩擦时物体由A沿曲线运动到B,克服重力做的功大于1 J | |
| D. | 物体运动,重力做的功是-1J,物体重力势能增加1J |
1. 如图,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板(A位置)上,随跳板一同向下运动到最低点(B位置).对于运动员从开始与跳板接触到运动至最低点的过程中,下列说法正确的是( )
如图,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板(A位置)上,随跳板一同向下运动到最低点(B位置).对于运动员从开始与跳板接触到运动至最低点的过程中,下列说法正确的是( )
 如图,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板(A位置)上,随跳板一同向下运动到最低点(B位置).对于运动员从开始与跳板接触到运动至最低点的过程中,下列说法正确的是( )
如图,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板(A位置)上,随跳板一同向下运动到最低点(B位置).对于运动员从开始与跳板接触到运动至最低点的过程中,下列说法正确的是( )| A. | 运动员到达最低点时,其所受外力的合力为零 | |
| B. | 在这个过程中,运动员的动能一直在减小 | |
| C. | 在这个过程中,跳板的弹性势能一直在增加 | |
| D. | 在这个过程中,运动员的机械能守恒 |
16. 如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
 如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )
如图,一个原来不带电的半径为r的空心金属球放在绝缘支架上,右侧放置一个电荷量为+Q的点电荷,点电荷到金属球表面的最近距离为2r,下列说法正确的是( )| A. | 金属球右侧感应出正电荷 | |
| B. | 感应起电后金属球总带电量为-Q | |
| C. | 金属球上的感应电荷在球心处激发的电场强度大小为k$\frac{Q}{9{r}^{2}}$ | |
| D. | 点电荷受到的库仑力大小为k$\frac{{Q}^{2}}{4{r}^{2}}$ |
 如图,粗细均匀、横截面积为S、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定量的热力学温度为T0的理想气体.开始时,活塞上方气体压强为p0,气柱长度为3L,活塞下方气柱长度为L,现将活塞上方抽成真空并密封,抽气过程中管内气体温度始终保持不变.活塞稳定时距玻璃管顶端的距离为L,求:
如图,粗细均匀、横截面积为S、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔.管内下部被活塞封住一定量的热力学温度为T0的理想气体.开始时,活塞上方气体压强为p0,气柱长度为3L,活塞下方气柱长度为L,现将活塞上方抽成真空并密封,抽气过程中管内气体温度始终保持不变.活塞稳定时距玻璃管顶端的距离为L,求: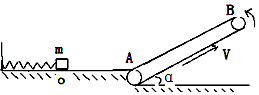 如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: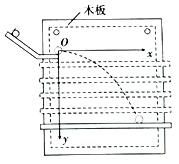 某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.
某同学在用如图的装置做“研究平抛物体运动”的实验,已知重力加速度为g,请按要求完成下列填空.