题目内容
11.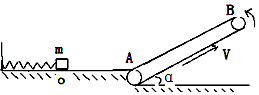 如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,在水平面上有一轻质弹簧,其左端与竖直墙壁相连,在水平面右侧有一倾斜的传送带与水平面在A点平滑连接,当传送带静止时.一质量m=1kg可视为质点的物体压缩弹簧到O点(与弹簧不拴接),然后静止释放,最后物体到达传送带上端B点时的速率刚好为零.已知物体与水平面及物体与传送带的动摩擦因数均为0.5,水平面OA段长L=1m皮带轮AB之间长S=1.8m,传送带与水平面之间的夹角α为37°,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)物体经过A点时的速率
(2)释放物体之前弹簧所具有的弹性势能
(3)若皮带轮以V=5m/s的速率逆时针匀速转动,求物体从A到B与传送带之间由于摩擦而产生的热量.
分析 (1)物体从A运动到B的过程,运用动能定理列式,即可求解物体经过A点时的速率;
(2)根据功能关系,即可求解释放物体之前弹簧所具有的弹性势能;
(3)根据牛顿第二定律和运动学公式结合,分段求出时间和位移;最后结合公式Q=f•△S求解热量.
解答 解:(1)物体从A运动到B,由动能定理得:
-μmgcosα•s-mgs•sinα=0-$\frac{1}{2}m{v}_{A}^{2}$
代入数据解得:vA=6m/s
(2)由功能关系可得:Ep=μmgL+$\frac{1}{2}m{v}_{A}^{2}$
代入数据解得:弹簧所具有的弹性势能为:Ep=23J
(3)设物体从A到B的时间为t,由vA=at 代入数据得:t=0.6s
由 s传=vt代入数据得:s传=3m
由Q=μmgcos37°•s相
又s相=s传+L
解得:Q=19.2J
答:(1)物体经过A点时的速率6m/s;
(2)释放物体之前弹簧所具有的弹性势能23J;
(3)物体与传送带之间由于摩擦而产生的热量19.2J.
点评 本题首先要理清物体的运动过程,其次要准确把握每个过程所遵守的物理规律,掌握动能定理的应用,注意求解摩擦产生热量时要用相对位移.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
4.发现万有引力定律与测定万有引力常量的科学家分别是( )
| A. | 开普勒 牛顿 | B. | 牛顿 卡文迪许 | C. | 牛顿 伽利略 | D. | 伽利略 第谷 |
19.2016年10月19日,“神舟十一号”飞船与“天宫二号”实验室实现自动交会对接,形成的“天神组合体”开始了长达30天的组合飞行,再一次创造了中国载人航天的新纪录.若在实现交会对接过程中,先使“神舟十一号”飞船沿椭圆轨道运行,且让椭圆轨道的远地点在“天宫二号”等待交会对接的近似正圆轨道上,然后在“神舟十一号”运行到远地点附近时进行对接,并使“天神组合体”能沿“天宫二号”原来的近似正圆轨道运动.对于这个对接过程,“神舟十一号”沿椭圆轨道运行到达远地点时应做出的调整,下列说法中正确的是( )
| A. | 需要适当减速 | B. | 需要适当加速 | ||
| C. | 需要先减速再加速 | D. | 需要适当改变速度方向 |
16.如图所示,一均匀带正电的无限长绝缘细杆水平放置,细杆上方有A、B、C三点,三点均与细杆在同一竖直平面内,且三点到细杆的距离满足rA=rB<rC,则( )


| A. | A、B、C三点电势φA=φB<φC | |
| B. | 将一负电荷从A点移到C点,电荷电势能一定增加 | |
| C. | A、B、C三点电场强度方向相同 | |
| D. | 在A点,若电子以一垂直于纸面向外的速度飞出,电子一定做匀速圆周运动 |
20.氢原子的能级如图所示,下列说法正确的是( )


| A. | 一个氢原子从n=4的激发态跃迁到基态时,有可能辐射出6种不同频率的光子,这时电子动能减少,原子势能减少 | |
| B. | 已知可见光的光子能量范围约是1.62eV~3.11eV,处于n=3能级的氢原子可以吸收任意频率的紫外线,并发生电离 | |
| C. | 有一群处于n=4能级的氢原子,如果原子n=2向n=1跃迁所发生的光正好使某种金属材料产生光电效应,则这群氢原子发出的光谱中共有两条谱线能使该金属产生光电效应 | |
| D. | 有一群处于n=4能级的氢原子,如果原子n=2向n=1跃迁所发生的光正好使某种金属材料产生光电效应,从能级n=4向n=1发出的光照射该金属材料,所产生的光电子的最大初动能为2.55eV |

 水平固定的汽缸A和竖直固定的汽缸B内壁光滑长度均为4L、横截面积均为S,A、B之间由一段容积可忽略的带阀门的细管相连,整个装置置于温度27℃、大气压为p0的环境中,活塞C、D的质量及厚度均忽略不计,缸内气体均为理想气体,原长3L、劲度系数k=$\frac{2{p}_{0}S}{L}$的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点,开始时活塞C距汽缸A的底部为1.5L,活塞D距汽缸B的底部为L.求:
水平固定的汽缸A和竖直固定的汽缸B内壁光滑长度均为4L、横截面积均为S,A、B之间由一段容积可忽略的带阀门的细管相连,整个装置置于温度27℃、大气压为p0的环境中,活塞C、D的质量及厚度均忽略不计,缸内气体均为理想气体,原长3L、劲度系数k=$\frac{2{p}_{0}S}{L}$的轻弹簧,一端连接活塞C、另一端固定在位于汽缸A缸口的O点,开始时活塞C距汽缸A的底部为1.5L,活塞D距汽缸B的底部为L.求: 如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1.6kg的无人机,其动力系统所能提供的最大升力F=36N,已知每个旋翼所能提供的升力Fi=kωi2,(k为常数,ωi为旋翼转动的角速度),运动过程中所受空气阻力大小恒为f=4N,取g=10m/s2.
如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=1.6kg的无人机,其动力系统所能提供的最大升力F=36N,已知每个旋翼所能提供的升力Fi=kωi2,(k为常数,ωi为旋翼转动的角速度),运动过程中所受空气阻力大小恒为f=4N,取g=10m/s2.