题目内容
19. 某汽车训练场地有如图设计,在平直的道路上,依次有编号为A、B、C、D、E的五根标志杆,相邻杆之间的距离△L=12.0m.一次训练中,学员驾驶汽车以57.6km/h的速度匀速向标志杆驶来,教练与学员坐在同排观察并记录时间.当教练经过O点时向学员发出指令:“立即刹车”,同时用秒表开始计时.忽略反应时间,刹车后汽车做匀减速直线运动,停在D标杆附近.教练记录自己经过C杆时秒表的读数为tC=6.0s,已知LOA=36m,教练距车头的距离△s=1.5m.求:
某汽车训练场地有如图设计,在平直的道路上,依次有编号为A、B、C、D、E的五根标志杆,相邻杆之间的距离△L=12.0m.一次训练中,学员驾驶汽车以57.6km/h的速度匀速向标志杆驶来,教练与学员坐在同排观察并记录时间.当教练经过O点时向学员发出指令:“立即刹车”,同时用秒表开始计时.忽略反应时间,刹车后汽车做匀减速直线运动,停在D标杆附近.教练记录自己经过C杆时秒表的读数为tC=6.0s,已知LOA=36m,教练距车头的距离△s=1.5m.求:(1)刹车后汽车做匀减速运动的加速度大小a;
(2)汽车停止运动时,车头离标志杆D的距离△x.
分析 (1)学员刹车后做匀减速运动.汽车从O到标志杆C的过程中分别列位移方程,即可求得加速度.
(2)先求出汽车从开始到停下运动的距离,在根据位移关系求汽车停止运动时车头前端面离D的距离.
解答 解:(1)汽车从O到标志杆C的过程中:
LOA+2△L=v0tC-$\frac{1}{2}a$tC2
解得:
a=2m/s2
(2)汽车从开始到停下运动的距离:
$x=\frac{{{v}_{0}}^{2}}{2a}$
可得x=64m
因此汽车停止运动时车头前端面在CD之间离D
LOA+3△L-△s-x=36+36-1.5-64=6.5m.
答:(1)车开始刹车后做匀减速直线运动的加速度大小a为2m/s2;
(2)汽车停止运动时车头前端面离D的距离为6.5m.
点评 此题要理解反应时间内汽车继续做匀速运动,还要养成画运动过程示意图,找位移之间的关系.此题有一定的难度

练习册系列答案
相关题目
9. 波速均为v=2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图甲、乙所示,其中P、Q处的质点均处于波峰.关于这两列波,下列说法正确的是( )
波速均为v=2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图甲、乙所示,其中P、Q处的质点均处于波峰.关于这两列波,下列说法正确的是( )
 波速均为v=2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图甲、乙所示,其中P、Q处的质点均处于波峰.关于这两列波,下列说法正确的是( )
波速均为v=2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图甲、乙所示,其中P、Q处的质点均处于波峰.关于这两列波,下列说法正确的是( )| A. | 从图示的时刻开始经过1.0 s,P质点沿x轴正方向发生的位移为2 m | |
| B. | 甲图中P处质点比M处质点先回到平衡位置 | |
| C. | 从图示时刻开始,P处质点比Q处质点后回到平衡位置 | |
| D. | 如果这两列波相遇,可以发生干涉现象 |
10. 某种角速度测量计结构如图所示,当整体系统绕轴OO′转动时,元件A发生位移并通过滑动变阻器输出电压U,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,系统静止时P在变阻器的最左端B点,当系统以角速度ω转动时,则( )
某种角速度测量计结构如图所示,当整体系统绕轴OO′转动时,元件A发生位移并通过滑动变阻器输出电压U,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,系统静止时P在变阻器的最左端B点,当系统以角速度ω转动时,则( )
 某种角速度测量计结构如图所示,当整体系统绕轴OO′转动时,元件A发生位移并通过滑动变阻器输出电压U,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,系统静止时P在变阻器的最左端B点,当系统以角速度ω转动时,则( )
某种角速度测量计结构如图所示,当整体系统绕轴OO′转动时,元件A发生位移并通过滑动变阻器输出电压U,电压传感器(传感器内阻无限大)接收相应的电压信号.已知A的质量为m,弹簧的劲度系数为k、自然长度为l,电源的电动势为E、内阻不计.滑动变阻器总长也为l,电阻分布均匀,系统静止时P在变阻器的最左端B点,当系统以角速度ω转动时,则( )| A. | 电路中电流随角速度的增大而增大 | |
| B. | 电路中电流随角速度的增大而减小 | |
| C. | 弹簧的伸长量为x=$\frac{mωl}{k-m{ω}^{2}}$ | |
| D. | 输出电压U与ω的函数式为U=$\frac{Em{ω}^{2}}{k-m{ω}^{2}}$ |
7. 密立根通过油滴实验测量了电子电荷.实验原理是让一个质量为m,带电量为q的油滴处在二块平行极板之间,向上、向下作匀速运动,如图所示.通过测量油滴匀速上升、下降时的速度和该油滴的直径等物理量,计算油滴的带电量,从而测出电子电荷.下列关于密立根油滴实验的叙述中不正确的是( )
密立根通过油滴实验测量了电子电荷.实验原理是让一个质量为m,带电量为q的油滴处在二块平行极板之间,向上、向下作匀速运动,如图所示.通过测量油滴匀速上升、下降时的速度和该油滴的直径等物理量,计算油滴的带电量,从而测出电子电荷.下列关于密立根油滴实验的叙述中不正确的是( )
 密立根通过油滴实验测量了电子电荷.实验原理是让一个质量为m,带电量为q的油滴处在二块平行极板之间,向上、向下作匀速运动,如图所示.通过测量油滴匀速上升、下降时的速度和该油滴的直径等物理量,计算油滴的带电量,从而测出电子电荷.下列关于密立根油滴实验的叙述中不正确的是( )
密立根通过油滴实验测量了电子电荷.实验原理是让一个质量为m,带电量为q的油滴处在二块平行极板之间,向上、向下作匀速运动,如图所示.通过测量油滴匀速上升、下降时的速度和该油滴的直径等物理量,计算油滴的带电量,从而测出电子电荷.下列关于密立根油滴实验的叙述中不正确的是( )| A. | 平行极板一定要水平,通电时上极板接电源负极 | |
| B. | 实验时要选择质量、电量适当小一些的油滴 | |
| C. | 实验明确了电荷具有不连续性,即具有量子性 | |
| D. | 实验证明了任何带电体所带电荷都是基本电荷的整数倍 |
4.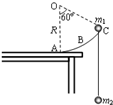 如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球(均可视为质点,m1>m2),挂在圆弧轨道光滑边缘C的两边,开始时m1位于C点,然后从静止释放.则( )
如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球(均可视为质点,m1>m2),挂在圆弧轨道光滑边缘C的两边,开始时m1位于C点,然后从静止释放.则( )
 如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球(均可视为质点,m1>m2),挂在圆弧轨道光滑边缘C的两边,开始时m1位于C点,然后从静止释放.则( )
如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球(均可视为质点,m1>m2),挂在圆弧轨道光滑边缘C的两边,开始时m1位于C点,然后从静止释放.则( )| A. | 在m1由C点下滑到A点的过程中两球速度大小始终相等 | |
| B. | 在m1由C点下滑到A点的过程中m1的速率始终比m2的速率大 | |
| C. | 若m1恰好能沿圆弧下滑到A点,则m1=2m2 | |
| D. | 若m1恰好能沿圆弧下滑到A点,则m1=3m2 |
11. 如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
 如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )
如图是煤气泄漏报警装置原理图,R1是对煤气敏感的半导体元件,其电阻随煤气浓度的增加而减小,R2是一可变电阻.在ac间接12V的恒定电压,bc间接报警器.当煤气浓度增加到一定值时报警器发出警告.则( )| A. | 减小R2的阻值,b点的电势升高 | |
| B. | 当煤气的浓度升高时,b点的电势降低 | |
| C. | 适当减小ac间的电压,可以提高报警器的灵敏度 | |
| D. | 调节R2的阻值能改变报警器启动时煤气浓度的临界值 |
 一半径为R的圆筒的横截面如图所示,其圆心为O.筒内有垂直于纸面向里的匀强磁场,磁感应强度为B.圆筒下面有相距为d的平行金属板M、N,M、N板接在如图所示的电路中,电源内阻为r0,定值电阻阻值为R1.当滑动变阻器R连入电路的电阻为0.质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S沿半径SO方向射入磁场中,粒子与圆筒发生两次碰撞后仍从S孔射出,设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下,
一半径为R的圆筒的横截面如图所示,其圆心为O.筒内有垂直于纸面向里的匀强磁场,磁感应强度为B.圆筒下面有相距为d的平行金属板M、N,M、N板接在如图所示的电路中,电源内阻为r0,定值电阻阻值为R1.当滑动变阻器R连入电路的电阻为0.质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S沿半径SO方向射入磁场中,粒子与圆筒发生两次碰撞后仍从S孔射出,设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下, 如图所示,工人通过两条传送带将质量为m的货物运送到高处,已知传送带1匀速运动的速度为v,传送带2的长度为L.将货物无初速度地放在传送带1的左端,到达右端前已经匀速运动,货物从传送带1过渡到传送带2时速度大小不变.某次传送带2因故障停转,工人发现货物沿传送带2向上滑行的最大距离为$\frac{3L}{5}$.
如图所示,工人通过两条传送带将质量为m的货物运送到高处,已知传送带1匀速运动的速度为v,传送带2的长度为L.将货物无初速度地放在传送带1的左端,到达右端前已经匀速运动,货物从传送带1过渡到传送带2时速度大小不变.某次传送带2因故障停转,工人发现货物沿传送带2向上滑行的最大距离为$\frac{3L}{5}$. 如图所示,上、下表面平行的玻璃砖的厚度为d,长度为L,下表面为镀银反射面,一束激光从上表面AB的中点射入,入射角为i,恰好从A点射出,光在真空中的光速为c,求:
如图所示,上、下表面平行的玻璃砖的厚度为d,长度为L,下表面为镀银反射面,一束激光从上表面AB的中点射入,入射角为i,恰好从A点射出,光在真空中的光速为c,求: