题目内容
1．
如图，倾角θ=53°的斜面固定在水平地面上，斜面下端有一挡板M，一轻质弹簧的下端固定在挡板M上，在自然长度下，弹簧的上端在P点处，斜面上P点以上的部分为光滑，P点以下的部分与小物块间的动摩擦因数μ=0.5，一质量m=2.0kg的小物块从斜面上的Q点由静止开始下滑，Q点与P点间的距离l=1.0cm，重力加速度g=10m/s2，sin53°=0.8，cos53°=0.6，求：（1）小物块第一次运动到P点的速度大小；
（2）小物块与弹簧接触后，弹簧的最大压缩量为x=0.2m，整个过程中弹簧始终在弹性限度内，则弹簧的最大弹性势能是多少？
分析 （1）对从Q到P过程运用动能定理列式求解即可；
（2）对从Q到弹簧压缩量最大的过程，根据功能关系可求弹簧的最大弹性势能．
解答 解：（1）对从Q到P过程，根据动能定理，有：mgsinθ•l=$\frac{1}{2}$mv2
代入数据解得：v=$\sqrt{2glsin5{3}^{0}}$=$\sqrt{2×10×0.01×0.8}$=0.4m/s
（2）对从Q到弹簧压缩量最大的过程，根据功能关系，有：mgsinθ•（x+l）-μmgcosθ•l-EP=0
解得：EP=mgsinθ•（x+l）-μmgcosθ•x=2×10×0.8×（0.01+0.2）-0.5×2×10×0.6×0.2=2.16J
答：（1）物块A第一次运动到P点的速度大小为0.4m/s；
（2）在弹簧压缩过程中弹簧具有的最大弹性势能为2.16J．
点评 本题关键灵活选择过程，多次根据动能定理和功能关系列式求解，注意重力和弹力做功与路径无关，摩擦力做功与路径有关．
练习册系列答案
相关题目
12．
如图所示，质为m的一辆小汽车从水平地面AC上的A点沿斜坡匀速行驶到B点．B距水平面高h，以水平地面为零势能面，重力加速度为g．小汽车从A点运动到B点的过程中（空气阻力不能忽略），下列说法正确的是（ ）
如图所示，质为m的一辆小汽车从水平地面AC上的A点沿斜坡匀速行驶到B点．B距水平面高h，以水平地面为零势能面，重力加速度为g．小汽车从A点运动到B点的过程中（空气阻力不能忽略），下列说法正确的是（ ）| A． | 合外力做功为零 | B． | 合外力做功为mgh | ||
| C． | 小汽车的机城能增加量为mgh | D． | 牵引力做功为mgh |
13．起重机用轻绳以恒定的功率P使质量为m的物体从静止开始竖直向上运动，经过一段时间t达到最大速度v，不计空气阻力，则在t这段时间内（ ）
| A． | 物体做匀加速运动 | B． | 绳子拉力保持不变 | ||
| C． | 起重机做的功为Pt | D． | 起重机做的功为$\frac{1}{2}$mv2 |
某同学设计了如图1所示的电路来测定一半导体电阻丝的电阻率．
6．
一个木块沿倾角为α的斜面刚好能匀速下滑，若这个斜面倾角增大到β（α＜β＜90°），则木块下滑加速度大小为（ ）
一个木块沿倾角为α的斜面刚好能匀速下滑，若这个斜面倾角增大到β（α＜β＜90°），则木块下滑加速度大小为（ ）| A． | gsinβ | B． | gsin（β-α） | C． | g（sinβ-tanαcosβ） | D． | g（sinβ-tanα） |
13．
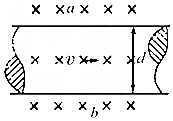为了诊断病人的心脏功能和动脉血液黏稠情况，需测量血管中血液的流量，如图所示为电磁流量计示意图，将血管置于磁感应强度为B的磁场中，测得血管两侧a、b两点间电压为u，已知血管的直径为d，则血管中血液的流量Q（单位时间内流过的体积）为（ ）
为了诊断病人的心脏功能和动脉血液黏稠情况，需测量血管中血液的流量，如图所示为电磁流量计示意图，将血管置于磁感应强度为B的磁场中，测得血管两侧a、b两点间电压为u，已知血管的直径为d，则血管中血液的流量Q（单位时间内流过的体积）为（ ）| A． | $\frac{u}{Bd}$ | B． | $\frac{πdu}{B}$ | C． | $\frac{πdu}{4B}$ | D． | $\frac{πd2u}{4B}$ |
质量为m的带电小球用绝缘丝线悬挂于O点，并处于水平向左、大小为E的匀强电场中，小球静止时丝线与竖直方向的夹角为θ，如图所示；