题目内容
4. 在竖直平面内有一个粗糙的$\frac{1}{4}$圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,则下列正确的是( )
在竖直平面内有一个粗糙的$\frac{1}{4}$圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,则下列正确的是( )| A. | 小滑块离开轨道时的速度大小为2.0m/s | |
| B. | 小滑块运动到轨道最低点时,对轨道的压力大小为2.0N | |
| C. | 小滑块在轨道上运动的过程中,克服摩擦力所做的功为0.2J | |
| D. | 小滑块落到C点时,重力的瞬时功率为$\sqrt{13}$W |
分析 根据平抛运动的规律求出平抛运动的初速度即小滑块离开轨道时的速度大小;根据牛顿第二定律求出小滑块经过最低点时对轨道的压力;由动能定理求出小滑块在轨道上克服摩擦力所做的功;重力的瞬时功率根据$mg{v}_{y}^{\;}$计算.
解答 解:A、小滑块离开轨道后做平抛运动,竖直方向$h=\frac{1}{2}g{t}_{\;}^{2}$,得$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.45}{10}}=0.3s$,水平$x={v}_{0}^{\;}t$,得${v}_{0}^{\;}=\frac{x}{t}=\frac{0.6}{0.3}m/s=2m/s$,故A正确.
B、小滑块经过轨道最低点时,根据向心力公式得${F}_{N}^{\;}-mg=m\frac{{v}_{0}^{2}}{R}$,代入数据解得${F}_{N}^{\;}=2.0N$,故B正确.
C、小滑块在轨道上运动过程中运用动能定理$mgR-{W}_{f}^{\;}=\frac{1}{2}m{v}_{0}^{2}-0$,代入数据解得${W}_{f}^{\;}=0.2J$,故C正确.
D、滑块落到C点时${v}_{y}^{\;}=gt=3m/s$,重力的瞬时功率$P=mg{v}_{y}^{\;}=3W$,故D错误.
故选:ABC
点评 本题考查了平抛运动、向心力公式、动能定理、瞬时功率的有关计算,关键是基本规律和基本概念要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
 如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )
如图所示,吊在天花板下的导热汽缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定量的理想气体.起初各部分均静止不动,外界大气压保持不变,针对汽缸内的气体,当状态缓慢发生变化时,下列判断正确的是( )| A. | 迅速向下拉动活塞,缸内气体温度降低 | |
| B. | 当活塞向下移动时,外界一定对气体做正功 | |
| C. | 若汽缸导热良好,保持环境温度不变,缓慢增加重物的质量,气体一定会吸热 | |
| D. | 缓慢增加重物的质量,欲保持气体体积不变,必须设法减少气体的内能 | |
| E. | 环境温度升高,气体的压强一定增大 |
12. 如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
 如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )| A. | 飞船在P点的加速度一定是$\frac{g}{9}$ | |
| B. | 飞船经过P点的速度一定是 $\sqrt{\frac{gR}{3}}$ | |
| C. | 飞船经过P点的速度小于 $\sqrt{\frac{gR}{3}}$ | |
| D. | 飞船经过P点时,若变轨为半径为3R的圆周运动,需要制动减速 |
19.如图所示,为一物体运动的速度一时间图象,下列说法正确的是( )


| A. | 物体在0~1s内,a=4m/s2 | |
| B. | 物体在2~3s内的加速度与在3~4s内的加速度相同 | |
| C. | 物体在3~4s秒内的加速度与4~5s内的加速度相同 | |
| D. | 物体在5s内总位移为4m |
9.在以下四种交流电中,有效值最大的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
19. 如图甲所示,用竖直向上的力F拉静止在水平地面上的一物体,物体在向上运动的过程中,其机械能E与位移x的关系如图乙,其中AB为曲线,其余部分为直线,下列说法正确的是( )
如图甲所示,用竖直向上的力F拉静止在水平地面上的一物体,物体在向上运动的过程中,其机械能E与位移x的关系如图乙,其中AB为曲线,其余部分为直线,下列说法正确的是( )
 如图甲所示,用竖直向上的力F拉静止在水平地面上的一物体,物体在向上运动的过程中,其机械能E与位移x的关系如图乙,其中AB为曲线,其余部分为直线,下列说法正确的是( )
如图甲所示,用竖直向上的力F拉静止在水平地面上的一物体,物体在向上运动的过程中,其机械能E与位移x的关系如图乙,其中AB为曲线,其余部分为直线,下列说法正确的是( )| A. | 0~x1过程中,物体所受拉力不变 | |
| B. | x1~x2过程中,物体的加速度先减小后增大 | |
| C. | 0~x3过程中,物体的动能先增大后减小 | |
| D. | 0~x2过程中,物体克服重力做功的功率一直增大 |
20. 甲、乙两车在同一水平直的道路上同向匀速行驶,甲车在前,乙车在后,在t=0时刻甲、乙两车相距s=8m,并同时开始做匀减速运动,两车运动的v-t图象如图所示,则下列表述正确的是( )
甲、乙两车在同一水平直的道路上同向匀速行驶,甲车在前,乙车在后,在t=0时刻甲、乙两车相距s=8m,并同时开始做匀减速运动,两车运动的v-t图象如图所示,则下列表述正确的是( )
 甲、乙两车在同一水平直的道路上同向匀速行驶,甲车在前,乙车在后,在t=0时刻甲、乙两车相距s=8m,并同时开始做匀减速运动,两车运动的v-t图象如图所示,则下列表述正确的是( )
甲、乙两车在同一水平直的道路上同向匀速行驶,甲车在前,乙车在后,在t=0时刻甲、乙两车相距s=8m,并同时开始做匀减速运动,两车运动的v-t图象如图所示,则下列表述正确的是( )| A. | 甲、乙减速过程的加速度之比为1:2 | |
| B. | 在t=4s时,乙车在甲车前面 | |
| C. | 在4s~8s之间两车之间距离不断增大 | |
| D. | 在t=12s时甲车静止,以后乙车追上甲车再次相遇 |
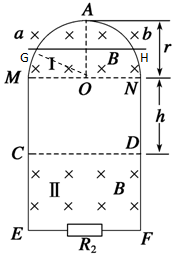 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2. 如图所示,有质量为m1=2kg、m2=3kg的两个物体放置于水平地面上,它们与地面的动摩擦因数分别为μ1=0.2,μ2=0.1.用F=22N的水平推力推两物体,使它们由静止开始一起向右运动,经过一段时间后撤去力F,当两物块都停止运动后,相距△x=6.75m.已知重力加速度g=10m/s2,求力F作用的时间t?
如图所示,有质量为m1=2kg、m2=3kg的两个物体放置于水平地面上,它们与地面的动摩擦因数分别为μ1=0.2,μ2=0.1.用F=22N的水平推力推两物体,使它们由静止开始一起向右运动,经过一段时间后撤去力F,当两物块都停止运动后,相距△x=6.75m.已知重力加速度g=10m/s2,求力F作用的时间t?