题目内容
12. 如图所示,半径为R的光滑圆弧轨道放置在竖直平面内,A、C是轨道的两个端点,A点与圆心O等高,C点和圆心O点的连线与竖直方向的夹角θ=60°,B点处在圆弧轨道的最低点.现有两个半径均为r(r<R)的小球1和小球2,其中小球2静止在B点.把小球1从A点由静止释放,到达最低点B处与小球2发生弹性碰撞,为使得小球2能离开圆弧轨道,小球2与小球1的质量之比$\frac{{m}_{2}}{{m}_{1}}$应满足什么条件?
如图所示,半径为R的光滑圆弧轨道放置在竖直平面内,A、C是轨道的两个端点,A点与圆心O等高,C点和圆心O点的连线与竖直方向的夹角θ=60°,B点处在圆弧轨道的最低点.现有两个半径均为r(r<R)的小球1和小球2,其中小球2静止在B点.把小球1从A点由静止释放,到达最低点B处与小球2发生弹性碰撞,为使得小球2能离开圆弧轨道,小球2与小球1的质量之比$\frac{{m}_{2}}{{m}_{1}}$应满足什么条件?
分析 小球1从A到B的过程中,机械能守恒,据此求出到达B处获得的速度,在B处小球1和小球2发生弹性碰撞,根据动量守恒定律以及机械能守恒定律求出碰撞后B的速度,小球2从B到C得过程中,机械能守恒,要保证在C点的速度大于0,据此求解即可.
解答 解:小球1从A到B的过程中,机械能守恒,到达B处获得的速度为v1,则有:
${m}_{1}gR=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}$
在B处小球1和小球2发生弹性碰撞,设碰撞后的速度分别为v1′和v2′,以v1速度方向为正方向,根据动量守恒定律得:
m1v1=m1v1′+m2v2′,
根据机械能守恒定律得:
${\frac{1}{2}m}_{1}{{v}_{1}}^{2}={\frac{1}{2}m}_{1}{v}_{1}{′}^{2}+{\frac{1}{2}m}_{2}{v}_{2}{′}^{2}$
小球2从B到C得过程中,机械能守恒,要保证在C点的速度大于0,则有:
$\frac{1}{2}{m}_{2}{v}_{2}{′}^{2}>{m}_{2}gR(1-cosθ)$
联立解得:$\frac{{m}_{2}}{{m}_{1}}<2\sqrt{2}-1$
答:为使得小球2能离开圆弧轨道,小球2与小球1的质量之比$\frac{{m}_{2}}{{m}_{1}}$应满足$\frac{{m}_{2}}{{m}_{1}}<2\sqrt{2}-1$.
点评 本题主要考查了机械能守恒定律以及动量守恒定律的直接应用,知道弹性碰撞过程中,机械能守恒,难度适中.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2. 如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长,小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长,小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
 如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长,小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长,小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )| A. | 小球可以返回到出发点A处 | |
| B. | 弹簧具有的最大弹性势能为$\frac{1}{2}$mv2 | |
| C. | 撤去弹簧,小球可以在直杆上处于静止 | |
| D. | aA-aC=g |
3. 如图,用三条细线悬挂的水平圆形线圈共有N匝,线圈由粗细均匀、单位长度质量为2克的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平,在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO′垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度B的方向与水平线成60°角,线圈中通过的电流为0.1A,要使三条细线上的张力为零,重力加速度g取10m/s2.则磁感应强度B的大小应为( )
如图,用三条细线悬挂的水平圆形线圈共有N匝,线圈由粗细均匀、单位长度质量为2克的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平,在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO′垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度B的方向与水平线成60°角,线圈中通过的电流为0.1A,要使三条细线上的张力为零,重力加速度g取10m/s2.则磁感应强度B的大小应为( )
 如图,用三条细线悬挂的水平圆形线圈共有N匝,线圈由粗细均匀、单位长度质量为2克的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平,在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO′垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度B的方向与水平线成60°角,线圈中通过的电流为0.1A,要使三条细线上的张力为零,重力加速度g取10m/s2.则磁感应强度B的大小应为( )
如图,用三条细线悬挂的水平圆形线圈共有N匝,线圈由粗细均匀、单位长度质量为2克的导线绕制而成,三条细线呈对称分布,稳定时线圈平面水平,在线圈正下方放有一个圆柱形条形磁铁,磁铁的中轴线OO′垂直于线圈平面且通过其圆心O,测得线圈的导线所在处磁感应强度B的方向与水平线成60°角,线圈中通过的电流为0.1A,要使三条细线上的张力为零,重力加速度g取10m/s2.则磁感应强度B的大小应为( )| A. | 4T | B. | 0.4T | C. | $\frac{0.4\sqrt{3}}{3}$T | D. | 0.4$\sqrt{3}$T |
20.关于物理学史,下列说法正确的是( )
| A. | 法拉第通过实验研究得出真空中两点电荷之间相互作用力的规律 | |
| B. | 元电荷e的数值最早是由汤姆生测得 | |
| C. | 法拉第采用了一种简洁的方法描述电场,那就是电场线 | |
| D. | 奥斯特发现了磁生电的现象 |
17. 如图为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
如图为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
 如图为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
如图为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )| A. | 如果y表示加速度,则面积等于质点在t0时刻的速度 | |
| B. | 如果y表示力估功的功率,则面积等于该力在相应时间内所做的功 | |
| C. | 如果y表示通过用电器的电流,则面积等于在相应时间内该用电器消耗的电能 | |
| D. | 如果y表示变化磁场在金属线圈中产生的电动势,则面积等于该磁场在相应时间内磁感应强度的变化量 |
1. 如图所示,圆O的半径为1m,一质点从圆上A点,以1m/s的速度沿圆周顺指针转过180°到达B点,质点的平均速度大小为( )
如图所示,圆O的半径为1m,一质点从圆上A点,以1m/s的速度沿圆周顺指针转过180°到达B点,质点的平均速度大小为( )
 如图所示,圆O的半径为1m,一质点从圆上A点,以1m/s的速度沿圆周顺指针转过180°到达B点,质点的平均速度大小为( )
如图所示,圆O的半径为1m,一质点从圆上A点,以1m/s的速度沿圆周顺指针转过180°到达B点,质点的平均速度大小为( )| A. | 1m/s | B. | $\frac{1}{π}$m/s | C. | $\frac{π}{2}$m/s | D. | $\frac{2}{π}$m/s |
2.中国最新研制的“长征六号”运载火箭2015年9月20日首次发射,成功将20颗微小人造卫星送入预定轨道,缔造“一箭多星”发射的亚洲新纪录.假设某颗卫星运行在轨道半径是地球半径n倍的圆形轨道上,由此可知( )
| A. | 该卫星运行的向心加速度大小是地球表面重力加速度的$\frac{1}{{n}^{2}}$ | |
| B. | 该卫星运行的向心加速度大小是地球表面重力加速度的$\frac{1}{n}$ | |
| C. | 该卫星的运行速度大小是第一宇宙速度大小的$\frac{1}{{n}^{2}}$ | |
| D. | 该卫星的运行速度大小是第一宇宙速度大小的$\frac{1}{\sqrt{n}}$ |




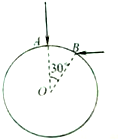 半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求:
半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求: