题目内容
4.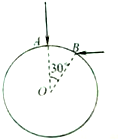 半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求:
半径为R玻璃圆柱体,截面如图所示,圆心为O,在同一截面内,两束相 互垂直的同种单色光射向圆柱面的A、B两点,其中一束沿AO方向,∠AOB=30°,玻璃对此单色光的折射率n=$\sqrt{3}$,真空中光速为c.求:(1)光线从B点射入到第一次射出圆柱面所用时间;
(2)求两束光线经圆柱体后第一次射出的光线的交点(或延长线的交点)与A点的距离.
分析 (1)由几何知识得到光线B的入射角,由折射定律求出折射角,即可画出光路图.根据几何知识求出光线在圆柱体传播的距离,由v=$\frac{c}{n}$求光线光在圆柱体中传播的速度大小,即可求出传播的时间.
(2)根据几何知识求解两条光线经圆柱体后第一次射出的光线的交点与A点的距离.
解答  解:(1)光线从B点射入,由几何知识可知,入射角 θ1=60°
解:(1)光线从B点射入,由几何知识可知,入射角 θ1=60°
设折射角θ2,根据折射定律得 n=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$
得 θ2=30°
则BC=2Rcos30°=$\sqrt{3}$R
又因为光在圆柱体中传播的速度 v=$\frac{c}{n}$
所以光线从B点射入到第一次射出圆柱面所用时间 t=$\frac{BC}{v}$=$\frac{3R}{c}$
(2)A光射入和射出圆柱始终垂直于界面,不变向射出玻璃圆柱的折射角为0°
设射出折射角为θ3,由n=$\frac{sin{θ}_{3}}{sin{θ}_{2}}$
解得 θ3=60°
设光线从C点射出光反向延长线交A光于D点,由几何知识可知∠DOC为直角,则 DA=Ttan60°-R=($\sqrt{3}-1$)R
答:
(1)光线从B点射入到第一次射出圆柱面所用时间是$\frac{3R}{c}$;
(2)两束光线经圆柱体后第一次射出的光线的交点与A点的距离是($\sqrt{3}-1$)R.
点评 对于几何光学问题,准确作出光路图,结合几何知识进行分析和求解相关角度和距离是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.据天文学观测,某行星在距离其表面高度等于该行星半径3倍处有一颗同步卫星,已知该行星质量是地球质量的$\frac{1}{2}$,行星半径是地球半径的$\frac{1}{2}$,地球表面附近绕地球做匀速圆周运动的卫星周期为T1,该行星的自转周期为T2,则T1:T2为( )
| A. | 1:4 | B. | 2:3$\sqrt{3}$ | C. | 2:1 | D. | 1:8 |
9.一列客运列车以72km/h的速度沿一平直铁路运动,驾驶员发现正前方有一牧童骑着一头牛站在铁轨上玩耍,立刻刹车,刹车后列车以大小为0.4m/s2的加速度减速运动,恰好没发生车祸,忽略驾驶员的反应时间,则刚剎车时列车与牧童间的距离为( )
| A. | 250 m | B. | 500 m | C. | 750 m | D. | 1000 m |
16.一物体以某一初速度开始做匀减速直线运动直至停止,其总位移为s,当其位移为$\frac{1}{4}$s时,所用时间为t,则当其速度为$\frac{1}{4}$v0时,所用时间为( )
| A. | $\frac{\sqrt{3}}{2}$t | B. | t | C. | $\frac{3}{2}$t | D. | $\frac{6+3\sqrt{3}}{2}$t |
13. 如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
 如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )| A. | 20N,水平向左 | B. | 20N,水平向右 | C. | 10N,水平向左 | D. | 10N,水平向右 |
14.“神九”载人飞船与“天宫一号”成功对接及“蛟龙”号下潜突破7000米入选2012年中国十大科技进展新闻.若地球半径为R,把地球看做质量分布均匀的球体(质量分布均匀的球壳对球内任一质点的万有引力为零).“蛟龙”号下潜深度为d,“天宫一号”轨道距离地面高度为h,“蛟龙”号所在处与“天宫一号”所在处的重力加速度之比为( )
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d)(R+h)^{2}}{{R}^{3}}$ | D. | $\frac{(R-d)(R+h)}{{R}^{2}}$ |
 某同学为测定金属丝的电阻,做如下测量:
某同学为测定金属丝的电阻,做如下测量: 升旗手小明在国歌响起时开始升旗,当国歌结束时国旗恰好到旗杆顶端.已知国歌从响起到结束的时间是48s,升旗时国旗竖直向上运动22m.国旗先匀加速运动,再匀速运动,最后匀减速运动,国旗到达旗杆顶端时的速度恰好为零,其运动的v-t图如图所示.不计一切摩擦和绳质量,国旗质量m=2kg,g=l0m/s2.求:
升旗手小明在国歌响起时开始升旗,当国歌结束时国旗恰好到旗杆顶端.已知国歌从响起到结束的时间是48s,升旗时国旗竖直向上运动22m.国旗先匀加速运动,再匀速运动,最后匀减速运动,国旗到达旗杆顶端时的速度恰好为零,其运动的v-t图如图所示.不计一切摩擦和绳质量,国旗质量m=2kg,g=l0m/s2.求: 如图所示,半径为R的光滑圆弧轨道放置在竖直平面内,A、C是轨道的两个端点,A点与圆心O等高,C点和圆心O点的连线与竖直方向的夹角θ=60°,B点处在圆弧轨道的最低点.现有两个半径均为r(r<R)的小球1和小球2,其中小球2静止在B点.把小球1从A点由静止释放,到达最低点B处与小球2发生弹性碰撞,为使得小球2能离开圆弧轨道,小球2与小球1的质量之比$\frac{{m}_{2}}{{m}_{1}}$应满足什么条件?
如图所示,半径为R的光滑圆弧轨道放置在竖直平面内,A、C是轨道的两个端点,A点与圆心O等高,C点和圆心O点的连线与竖直方向的夹角θ=60°,B点处在圆弧轨道的最低点.现有两个半径均为r(r<R)的小球1和小球2,其中小球2静止在B点.把小球1从A点由静止释放,到达最低点B处与小球2发生弹性碰撞,为使得小球2能离开圆弧轨道,小球2与小球1的质量之比$\frac{{m}_{2}}{{m}_{1}}$应满足什么条件?