题目内容
13. 如图所示,倾角为θ=30°的斜面上,固定两条无限长的平行光滑导轨cd和ef,导轨的f端和d端之间接有一个阻值为R0=0.4Ω的电阻,导轨间距L=0.5m,在两根导轨上距离顶端均为L处,分别固定着两颗挡钉,使金属棒ab水平地静止放在导轨上(未连接).金属棒ab的质量为m=0.1kg,金属棒ab的电阻的r=0.1Ω,导轨电阻不计.若从和t=0时起,在空间中加上方向垂直于斜面向上的匀强磁场,磁感应强度B大小由零开始逐渐均匀增加,且磁感应强度的变化率$\frac{△B}{△t}$=2T/s.g=10m/s2,求:
如图所示,倾角为θ=30°的斜面上,固定两条无限长的平行光滑导轨cd和ef,导轨的f端和d端之间接有一个阻值为R0=0.4Ω的电阻,导轨间距L=0.5m,在两根导轨上距离顶端均为L处,分别固定着两颗挡钉,使金属棒ab水平地静止放在导轨上(未连接).金属棒ab的质量为m=0.1kg,金属棒ab的电阻的r=0.1Ω,导轨电阻不计.若从和t=0时起,在空间中加上方向垂直于斜面向上的匀强磁场,磁感应强度B大小由零开始逐渐均匀增加,且磁感应强度的变化率$\frac{△B}{△t}$=2T/s.g=10m/s2,求:(1)金属棒ab中感应电流的大小和方向;
(2)当金属棒ab刚离开挡钉时,感应电流通过金属棒ab产生的热.
分析 (1)由法拉第电磁感应定律和欧姆定律可以求出电流大小,由楞次定律判断出电流方向.
(2)整个的过程中ab棒始终不动,电路中的电流大小不变,根据平衡条件求出磁场B,然后求出时间,最后根据电热的公式即可求出结果.
解答 解:
(1)由法拉第电磁感应定律知电动势为E=ns$\frac{△B}{△t}$=2L2=2×0.52=0.5V
由欧姆定律得I=$\frac{E}{r+{R}_{0}}$=$\frac{0.5}{0.1+0.4}$=1A
由楞次定律判断出电流方向为adfba.
(2)分析ab棒受到重力、支持力和安培力的作用而处于平衡状态,由力的平衡条件知:
B1Il=mgsinθ时将要离开铁钉
得:B1=$\frac{mgsinθ}{IL}$=$\frac{0.1×10×\frac{1}{2}}{1×0.5}$T=1T;
时间为t=$\frac{{B}_{1}}{\frac{△B}{△t}}$=$\frac{1}{2}$=0.5s;
由Q=I2Rt知
ab上产生热量为Q=I2rt=12×0.1×0.5J=0.05J
答:(1)通过ab棒的电流的大小是1A,电流由b到a;
(2)感应电流通过金属棒ab产生的热0.05J.
点评 此题考查由法拉第电磁感应定律和欧姆定律、楞次定律和力学及能量的综合,属于综合性较强的题目.

练习册系列答案
相关题目
13.当线圈在磁场中处于中性面位置时,关于线圈平面与磁感线的位置关系,下列说法正确的是( )
| A. | 相互垂直 | B. | 相互平行 | C. | 夹角为45° | D. | 夹角为60° |
1.用测电笔测试通有交变电流的电气设备的金属外壳时,发现测电笔的氖管发光,其原因( )
| A. | 一定是电源连接到金属外壳上了 | |
| B. | 一定是与电源相连的机芯与金属外壳间绝缘不良,导致漏电所致 | |
| C. | 可能是该设备的金属外壳没有接地 | |
| D. | 可能是电源中的交变电流“通过”了由机芯和金属外壳构成的“电容器” |
8. 如图所示,水平放置的光滑平行金属导轨上有一质量为m的金属棒ab,金属棒与导轨接触良好,导轨一端连接电阻R,其它电阻均不计,磁感应强度为B的匀强磁场垂直于导轨平面向下,金属棒ab在一水平恒力F作用下由静止开始向右运动.则( )
如图所示,水平放置的光滑平行金属导轨上有一质量为m的金属棒ab,金属棒与导轨接触良好,导轨一端连接电阻R,其它电阻均不计,磁感应强度为B的匀强磁场垂直于导轨平面向下,金属棒ab在一水平恒力F作用下由静止开始向右运动.则( )
 如图所示,水平放置的光滑平行金属导轨上有一质量为m的金属棒ab,金属棒与导轨接触良好,导轨一端连接电阻R,其它电阻均不计,磁感应强度为B的匀强磁场垂直于导轨平面向下,金属棒ab在一水平恒力F作用下由静止开始向右运动.则( )
如图所示,水平放置的光滑平行金属导轨上有一质量为m的金属棒ab,金属棒与导轨接触良好,导轨一端连接电阻R,其它电阻均不计,磁感应强度为B的匀强磁场垂直于导轨平面向下,金属棒ab在一水平恒力F作用下由静止开始向右运动.则( )| A. | 随着ab运动速度的增大,其加速度也增大 | |
| B. | 无论ab做何种运动,它克服安培力做的功一定等于电路中产生的电能 | |
| C. | 外力F对ab做的功等于电路中产生的电能 | |
| D. | 当ab做匀加速运动时,外力F做功的功率等于电路中的电功率 |
2. 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )| A. | 电流表的示数为4.4A | |
| B. | 原线圈的输入功率为16W | |
| C. | 电压表的示数为20V | |
| D. | 通过电阻R的交变电流的频率为100Hz |
 滑板运动是青少年喜爱的一项活动.如图所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后经C点沿固定斜面向上运动至最高点D,B、C为圆弧的两端点,其连线水平,轨道半径R=1.0m,圆弧对应圆心角θ=106°,E为圆弧的最低点,斜面与圆弧相切于C点.已知滑板与斜面间的动摩擦因数为μ=$\frac{1}{3}$,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板),可视为质点,其质量m=1kg.求:
滑板运动是青少年喜爱的一项活动.如图所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后经C点沿固定斜面向上运动至最高点D,B、C为圆弧的两端点,其连线水平,轨道半径R=1.0m,圆弧对应圆心角θ=106°,E为圆弧的最低点,斜面与圆弧相切于C点.已知滑板与斜面间的动摩擦因数为μ=$\frac{1}{3}$,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板),可视为质点,其质量m=1kg.求: 如图所示.在oxy平面第一象限的OP直线上方.有场强大小为E、沿y轴负方向的匀强电场,在OP直线和OQ盧线的下方,有垂直纸面向外的匀强磁场.在y轴上的a点,将质量为m、电荷最为+q的带电微粒以速度v0水平射入电场,经过一段时间后带电粒子从c点以一定的速度垂直于OP直线进入匀强磁场,当粒子经过X轴时速度方向与X轴垂直,再经过一段时间,带电粒子到达y轴上的b点.试求带电粒从a点开始运动到b点所用的时间(已知a=37°,θ=53°,sin37°=0.6,sin53°=0.8.带电微粒的重力不计).
如图所示.在oxy平面第一象限的OP直线上方.有场强大小为E、沿y轴负方向的匀强电场,在OP直线和OQ盧线的下方,有垂直纸面向外的匀强磁场.在y轴上的a点,将质量为m、电荷最为+q的带电微粒以速度v0水平射入电场,经过一段时间后带电粒子从c点以一定的速度垂直于OP直线进入匀强磁场,当粒子经过X轴时速度方向与X轴垂直,再经过一段时间,带电粒子到达y轴上的b点.试求带电粒从a点开始运动到b点所用的时间(已知a=37°,θ=53°,sin37°=0.6,sin53°=0.8.带电微粒的重力不计).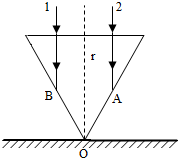 在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则:
在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则: