题目内容
8. 如图所示是真空中内径为R、外径为2R的空心玻璃柱体的横截面,空心部分为真空,一束在横截面内的单色平行光射向柱体外表面,其折射光线恰好未射入柱体空心部分,已知玻璃对该单色光的折射率为n=$\sqrt{3}$,求:
如图所示是真空中内径为R、外径为2R的空心玻璃柱体的横截面,空心部分为真空,一束在横截面内的单色平行光射向柱体外表面,其折射光线恰好未射入柱体空心部分,已知玻璃对该单色光的折射率为n=$\sqrt{3}$,求:(1)单色光射向柱体外表面的入射角;
(2)光在玻璃中传播的时间(已知真空中光速为c,不考虑多次反射).
分析 (1)由题意画出光路图,折射光线恰好未射入柱体空心部分,恰好发生了全反射,入射角等于临界角C.光线进入柱体外表面时由折射定律列式.由临界角公式sinC=$\frac{1}{n}$和几何关系确定折射角,则可求得折射角.
(2)由几何关系求出光在玻璃中传播的距离,由v=$\frac{c}{n}$求出光在玻璃中传播的速度,从而求得光在玻璃中传播的时间.
解答  解:由题意画出光路图如图.
解:由题意画出光路图如图.
光线进入柱体外表面时,由折射定律,有:n=$\frac{sini}{sinr}$
其折射光线恰好未射入柱体空心部分,恰好发生了全反射,入射角等于临界角C.则有:sinC=$\frac{1}{n}$
由正弦定理可得:$\frac{R}{sinr}$=$\frac{2R}{sin(180°-C)}$
联立解得:sini=0.5,i=30°
即单色光射向柱体外表面的入射角为30°.
(2)设光在玻璃中传播的距离为S.由正弦定理有:$\frac{0.5S}{sin(C-r)}$=$\frac{2R}{sin(180°-C)}$
结合n=$\frac{sini}{sinr}$得 sinr=$\frac{\sqrt{3}}{6}$,则有:cosr=$\sqrt{1-si{n}^{2}r}$=$\sqrt{\frac{11}{12}}$
sinC=$\frac{1}{n}$=$\frac{\sqrt{3}}{3}$,cosC=$\sqrt{1-si{n}^{2}C}$=$\sqrt{\frac{2}{3}}$
联立解得 S=$\frac{2(\sqrt{33}-\sqrt{6})R}{3}$
光在玻璃中传播的速度为 v=$\frac{c}{n}$=$\frac{\sqrt{3}}{3}$c
所以光在玻璃中传播的时间为 t=$\frac{S}{v}$=$\frac{2(\sqrt{11}-\sqrt{2})R}{c}$
答:(1)单色光射向柱体外表面的入射角是30°;
(2)光在玻璃中传播的时间是$\frac{2(\sqrt{11}-\sqrt{2})R}{c}$.
点评 本题是折射定律的应用,关键是画出光路图,运用几何知识研究角度关系,同时要掌握全反射的条件.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | 小船渡河的最短时间为40s | |
| B. | 当小船用最短航程渡河时,耗时为l00s | |
| C. | 小船渡河的最短航程为500m | |
| D. | 当小船用最短时间渡河时,航程为500m |
 如图所示,在固定矩形框架ABCD所围光滑水平面上,甲、乙两小球(均可视为质点)从AB边上同一位置同时以相同大小的初速度v运动,甲、乙速度方向与AB边夹角分别为α、β,且90°>α>β>0°,甲、乙两小球与矩形框架碰撞前后速度的大小不变,方向与边框的夹角相同,碰撞时间不计.假定小球不与四顶点碰撞,且小球相互之间不发生碰撞.甲、乙两球从AB边出发到第一次回到AB边所经历时间分别为t甲、t乙,则( )
如图所示,在固定矩形框架ABCD所围光滑水平面上,甲、乙两小球(均可视为质点)从AB边上同一位置同时以相同大小的初速度v运动,甲、乙速度方向与AB边夹角分别为α、β,且90°>α>β>0°,甲、乙两小球与矩形框架碰撞前后速度的大小不变,方向与边框的夹角相同,碰撞时间不计.假定小球不与四顶点碰撞,且小球相互之间不发生碰撞.甲、乙两球从AB边出发到第一次回到AB边所经历时间分别为t甲、t乙,则( )| A. | t甲>t乙 | |
| B. | t甲<t乙 | |
| C. | t甲=t乙 | |
| D. | 条件不足,无法判断t甲、t乙大小关系 |
| A. | 根据玻尔理论可知,一群氢原子从n=4能级向低能级跃迁最多可辐射6种频率的光子 | |
| B. | α射线、β射线、γ射线都是高速运动的带电粒子流 | |
| C. | 太阳辐射的能量主要来自太阳内部的核裂变反应 | |
| D. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小 |
 如图所示,在xOy坐标平面内有垂直于坐标平面的圆形有界匀强磁场,磁场边界圆的圆心在x轴上O1处,O1点坐标为(R,0),磁场边界圆与y轴相切于坐标原点O.在y轴上P点(0,$\frac{\sqrt{2}}{2}$R)沿x轴正向以初速度v0射出一个质量为m,电荷量大小为q的带正电的粒子,粒子进入磁场后经磁场偏转,从圆心O1正下方的Q点射出磁场,不计粒子所受的重力,则( )
如图所示,在xOy坐标平面内有垂直于坐标平面的圆形有界匀强磁场,磁场边界圆的圆心在x轴上O1处,O1点坐标为(R,0),磁场边界圆与y轴相切于坐标原点O.在y轴上P点(0,$\frac{\sqrt{2}}{2}$R)沿x轴正向以初速度v0射出一个质量为m,电荷量大小为q的带正电的粒子,粒子进入磁场后经磁场偏转,从圆心O1正下方的Q点射出磁场,不计粒子所受的重力,则( )| A. | 磁场方向垂直于纸面向里 | |
| B. | 粒子在磁场中做圆周运动的半径为$\frac{\sqrt{2}}{2}$R | |
| C. | 匀强磁场的磁感应强度大小为B=$\frac{m{v}_{0}}{qR}$ | |
| D. | 粒子从Q点射出的方向与x轴负方向的夹角为45° |

| A. | 质点在第2s末与第12s末的速度大小相等,方向相反 | |
| B. | 质点在第2s末与第12s末的加速度大小相等,方向相同 | |
| C. | 质点在0~5s内与第10s~15s内的位移大小相等,方向相同 | |
| D. | 质点在0~15s内的位移大小为5m |
 如图所示,已知两个小物块A、B的质量分别为2m和m,随圆盘一起在水平面内做匀速圆周运动,它们轨道半径之比为rA:rB=1:2,小物块A、B与圆盘之间的动摩擦因数相同,则下列说法正确的是( )
如图所示,已知两个小物块A、B的质量分别为2m和m,随圆盘一起在水平面内做匀速圆周运动,它们轨道半径之比为rA:rB=1:2,小物块A、B与圆盘之间的动摩擦因数相同,则下列说法正确的是( )| A. | 小物块A所受摩擦力的方向与轨迹圆相切 | |
| B. | 小物块A、B所受向心力大小相等 | |
| C. | 小物块A、B的向心加速度大小之比为1:2 | |
| D. | 若逐渐增大圆盘角速度,小物块B首先相对圆盘滑动 |
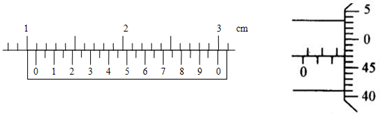 (1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm.
(1)图中游标卡尺的读数为10.90mm,螺旋测微器的读数为2.970mm. 如图所示,水平U形光滑框架,宽度为d=1m,MN间的电阻R=1.5Ω,导轨其它处电阻均不计,导体棒ab的质量m=0.2kg、电阻r=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向下.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到v=2m/s时,求:
如图所示,水平U形光滑框架,宽度为d=1m,MN间的电阻R=1.5Ω,导轨其它处电阻均不计,导体棒ab的质量m=0.2kg、电阻r=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向下.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到v=2m/s时,求: