题目内容
7. 如图所示,让物体分别同时从竖直圆上的P1、P2处由静止开始下滑,沿光滑的弦轨道P1A、
如图所示,让物体分别同时从竖直圆上的P1、P2处由静止开始下滑,沿光滑的弦轨道P1A、P2A滑到A处,P1A、P2A与竖直直径的夹角分别为θ1、θ2.则( )
| A. | 若两物体质量相同,则两物体所受的合外力之比为cosθ1:cosθ2 | |
| B. | 物体沿P1A、P2A下滑加速度之比为sinθ1:sinθ2 | |
| C. | 物体沿P1A、P2A下滑到A处的速度之比为cosθ1:cosθ2 | |
| D. | 物体沿P1A、P2A下滑的时间之比为1:1 |
分析 对物体受力分析求出物体所受的合外力,根据牛顿第二定律求出下滑的加速度;
通过位移以及加速度,根据位移时间公式求出运动的时间,从而得出末速度,然后进行比较得出答案.
解答 解:A、设两物体质量为m,物体受重力和支持力作用,
根据力的平衡条件可得,物体所受的合外力:
F合1=mgsin(90°-θ1)=mgcosθ1,
F合2=mgsin(90°-θ2)=mgcosθ2,
则两物体所受的合外力之比:
F合1:F合2=mgcosθ1:mgcosθ2=cosθ1:cosθ2,故A正确;
B、由牛顿第二定律得,
F合1=mgcosθ1=ma1,
F合2=mgcosθ2=ma2,
则物体沿P1A、P2A下滑加速度之比:
a1:a2=cosθ1:cosθ2,故B错误;
D、物体的位移x=2Rcosθ,加速度a=gcosθ,
由位移时间公式得,2Rcosθ=$\frac{1}{2}$gcosθt2,
解得t=$\sqrt{\frac{4R}{g}}$,与夹角无关,
故物体沿P1A、P2A下滑的时间之比:
t1:t2=1:1,故D正确;
C、由速度时间公式v=at得,物体沿P1A、P2A下滑到A处的速度之比:
v1:v2=cosθ1:cosθ2,故C正确.
故选:ACD.
点评 本题综合考查了牛顿第二定律和运动学公式相关应用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
2. 如图所示,五个木块并排放在水平地面上,它们的质量相同,与地面的摩擦不计,当用力F推第一块使它们共同加速运动时,第3块对第4块的推力为( )
如图所示,五个木块并排放在水平地面上,它们的质量相同,与地面的摩擦不计,当用力F推第一块使它们共同加速运动时,第3块对第4块的推力为( )
 如图所示,五个木块并排放在水平地面上,它们的质量相同,与地面的摩擦不计,当用力F推第一块使它们共同加速运动时,第3块对第4块的推力为( )
如图所示,五个木块并排放在水平地面上,它们的质量相同,与地面的摩擦不计,当用力F推第一块使它们共同加速运动时,第3块对第4块的推力为( )| A. | $\frac{F}{5}$ | B. | $\frac{2F}{5}$ | C. | $\frac{3F}{5}$ | D. | F |
19. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩至最短,若不计弹簧的质量和空气阻力,小球由b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩至最短,若不计弹簧的质量和空气阻力,小球由b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩至最短,若不计弹簧的质量和空气阻力,小球由b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩至最短,若不计弹簧的质量和空气阻力,小球由b→c的运动过程中( )| A. | 小球的动能逐渐减小 | B. | 小球的重力势能逐渐减小 | ||
| C. | 小球的机械能守恒 | D. | 小球的加速度先减小后增大 |
16. 如图所示,一根轻弹簧上端固定,下端悬挂一个物体.将物体从平衡位置竖直拉下一段距离后由静止释放,物体在竖直方向做简谐运动.设向下方向为正,则以下说法中正确的是( )
如图所示,一根轻弹簧上端固定,下端悬挂一个物体.将物体从平衡位置竖直拉下一段距离后由静止释放,物体在竖直方向做简谐运动.设向下方向为正,则以下说法中正确的是( )
 如图所示,一根轻弹簧上端固定,下端悬挂一个物体.将物体从平衡位置竖直拉下一段距离后由静止释放,物体在竖直方向做简谐运动.设向下方向为正,则以下说法中正确的是( )
如图所示,一根轻弹簧上端固定,下端悬挂一个物体.将物体从平衡位置竖直拉下一段距离后由静止释放,物体在竖直方向做简谐运动.设向下方向为正,则以下说法中正确的是( )| A. | 物体位移为正时,速度一定也为正,加速度一定为负 | |
| B. | 物体从最高处向最低处运动过程中,振幅先减小后增大 | |
| C. | 弹簧对物体的弹力变小时,物体所受回复力可能变大 | |
| D. | 物体从最低处向最高处运动过程中,物体的动能与弹簧的弹性势能之和一直减小 |
17.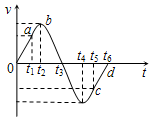 一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )
一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )
 一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )
一个小球在蹦床做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中Oa段和cd段为直线,则根据此图象可知,小孩和蹦床相接触的时间为( )| A. | t2-t4 | B. | t1-t4 | C. | t1-t5 | D. | t2-t3 |
 一物块重4.6N,对物块施一方向与竖直成37°的推力F,物块恰好沿竖直墙向上匀速滑动,物块与墙之间动摩擦因数为0.5,求推力F的大小.
一物块重4.6N,对物块施一方向与竖直成37°的推力F,物块恰好沿竖直墙向上匀速滑动,物块与墙之间动摩擦因数为0.5,求推力F的大小.