题目内容
4.以不同的初速度将两个物体A、B同时竖直向上抛出并开始计时,物体A所受空气阻力可忽略,物体B所受空气阻力大小与物体B的速率成正比,下列分别描述两物体运动的v-t图象和a-t图象,可能正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 空气阻力可忽略时,竖直上抛运动是初速度不为零的匀变速直线运动,加速度恒定不变,故其v-t图象是直线;有空气阻力时,根据牛顿第二定律判断加速度情况,v-t图象的斜率表示加速度,从而分析v-t图象和a-t图象即可.
解答 解:空气阻力不计时,物体只受重力,是竖直上抛运动,做匀变速直线运动,v-t图象是向下倾斜的直线,
有空气阻力时,上升阶段,根据牛顿第二定律,有:mg+f=ma,故a=g+$\frac{f}{m}$,由于阻力随着速度而减小,故加速度逐渐减小,最小值为g,
下降阶段,根据牛顿第二定律,有:mg-f=ma,故a=g-$\frac{f}{m}$,由于阻力随着速度而增大,故加速度减小,v-t图象的斜率表示加速度,故图线切线的斜率不断减小,图线与t轴的交点对应时刻的加速度为g,切线与虚线平行,A的加速度为g不变,B的加速度一直减小,当阻力等于重力时,加速度为0,做匀速直线运动,即最后应趋向于0,故B正确,ACD错误.
故选:B
点评 本题关键是明确v-t图象上某点的切线斜率表示加速度,知道有空气阻力时,速度为零时加速度为g.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
7. 如图所示,桌面离地高度为h.一质量为m的物块从桌面上方H高处由静止下落.以物块开始下落位置为参考平面,则物块落地时的重力势能及下落过程中重力对物块做的功分别为( )
如图所示,桌面离地高度为h.一质量为m的物块从桌面上方H高处由静止下落.以物块开始下落位置为参考平面,则物块落地时的重力势能及下落过程中重力对物块做的功分别为( )
 如图所示,桌面离地高度为h.一质量为m的物块从桌面上方H高处由静止下落.以物块开始下落位置为参考平面,则物块落地时的重力势能及下落过程中重力对物块做的功分别为( )
如图所示,桌面离地高度为h.一质量为m的物块从桌面上方H高处由静止下落.以物块开始下落位置为参考平面,则物块落地时的重力势能及下落过程中重力对物块做的功分别为( )| A. | mgh,mgH | B. | mg(H+h),mg(H+h) | C. | -mgh,mgH | D. | -mg(H+h),mg(H+h) |
8. 如图所示电路,把电阻、电感器、电容器并联接到某一交流电源上,此时三个电流表读数I1=I2=I3,下面关于电路的说法正确的是( )
如图所示电路,把电阻、电感器、电容器并联接到某一交流电源上,此时三个电流表读数I1=I2=I3,下面关于电路的说法正确的是( )
 如图所示电路,把电阻、电感器、电容器并联接到某一交流电源上,此时三个电流表读数I1=I2=I3,下面关于电路的说法正确的是( )
如图所示电路,把电阻、电感器、电容器并联接到某一交流电源上,此时三个电流表读数I1=I2=I3,下面关于电路的说法正确的是( )| A. | 若只增大交流电的频率,三个电流表读数都增大 | |
| B. | 若只增大交流电的电压,三个电流表的读数都增大 | |
| C. | 若将交流电源改成有效值相同的直流电源,三个电流表的读数不变 | |
| D. | 若将交流电源改成有效值相同的直流电源,I1、I2不变,I3=0 |
9.在离地高h处,同时自由下落和竖直向上抛出各一个小球,其中竖直上抛的小球初速度大小为v,不计空气阻力,重力加速度为g,两球落地的时间差为( )
| A. | $\frac{h}{v}$ | B. | $\frac{2h}{v}$ | ||
| C. | 2$\frac{v}{g}$ | D. | $\frac{v}{g}$+$\sqrt{\frac{{v}^{2}}{{g}^{2}}+\frac{2h}{g}}$-$\sqrt{\frac{2h}{g}}$ |
16.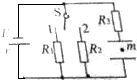 如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
 如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )| A. | $\frac{(Eq-ma)dg}{a(Eq-mgd)}$ | B. | $\frac{[qE-m(g-a)d]g}{(g-a)(qE-mgd)}$ | ||
| C. | $\frac{m(g-a)dg}{(Eq-mgd)}$ | D. | $\frac{mgdg}{(g-a)(Eq-mgd)}$ |
14.下列说法正确的是( )
| A. | 库仑通过大量实验分析,得到了真空中两个静止点电荷相互作用规律,并引入电场线形象地描述电荷周围的电场 | |
| B. | 物理学家法拉第通过实验证实了“磁生电”现象的存在,并总结出判断感应电流方向的规律 | |
| C. | 安培首先发现电流磁效应,总结了电流周围磁场方向的判断方法--安培定则 | |
| D. | 美国物理学家密立根利用实验,确定了电荷的不连续性,并测定了元电荷的数值 |
 如图所示,质量m=2kg的物体静止在水平桌面上,受到与水平地面夹角为θ=37°、大小F=10N的拉力作用,物体移动了s=2m,物体与地面间的动摩擦因数μ=0.3,g取10m/s2.求
如图所示,质量m=2kg的物体静止在水平桌面上,受到与水平地面夹角为θ=37°、大小F=10N的拉力作用,物体移动了s=2m,物体与地面间的动摩擦因数μ=0.3,g取10m/s2.求 如图所示是弹簧振子做简谐运动的频闪照片.频闪仪每隔0.05s闪光一次,闪光的瞬间振子被照亮,拍摄时底片从下向上匀速运动,因此在底片上留下了小球和弹簧的一系列的像,相邻两个像之间相隔0.05s,图中的两个坐标轴分别代表时间t和小球位移x,因此它就是小球在平衡位置附近往复运动时的位移-时间图象,即x-t图象.由图可知弹簧振子的振动周期约为1.1s,t=0.1s时振子的运动方向是沿x轴正向(或向右).
如图所示是弹簧振子做简谐运动的频闪照片.频闪仪每隔0.05s闪光一次,闪光的瞬间振子被照亮,拍摄时底片从下向上匀速运动,因此在底片上留下了小球和弹簧的一系列的像,相邻两个像之间相隔0.05s,图中的两个坐标轴分别代表时间t和小球位移x,因此它就是小球在平衡位置附近往复运动时的位移-时间图象,即x-t图象.由图可知弹簧振子的振动周期约为1.1s,t=0.1s时振子的运动方向是沿x轴正向(或向右).