��Ŀ����
20��ijͬѧ�÷�������һ�ڸɵ�صĵ綯�ƺ����裬�ֱ����������ģ�A������ɵ��һ��
B��������1������0��0.6A������r=0.2��
C��������2������0��0.6A������ԼΪ0.1��
D����ѹ��1������0��3V������δ֪
E����ѹ��2������0��15V������δ֪
F������������1��0��10����2A
G������������2��0��100����1A
H�����ء���������
��1�����������ص綯�ƺ������ʵ���У����ڵ������͵�ѹ�������Ӱ�죬�����������ϵͳ�����������ĵ������£�Ҫ������ȷ�ز�����صĵ綯�ƺ����裮��������������ѡ���ʵ������ģ�
A��B��D��F��H����дѡ��ǰ����ĸ����
��2��ʵ���·ͼӦѡ����ͼ�еļף���ס����ҡ�����

��3������ʵ���е������͵�ѹ����ʾ���õ�����ͼ����ʾ��U-Iͼ������������ʵ��ϵͳ���ɵ�صĵ綯��E=1.5V���ڵ���r=0.8����
���� ��1��ʵ����Ҫ�ܱ�֤��ȫ��ȷ��ѡ������
��2����ʵ��Ӧ���õ�����͵�ѹ�����ϲ�������ʵ��ԭ��ѡ���·ͼ��
��3����ԭ�����ñպϵ�·ŷķ���ɿɵó�����ʽ������ѧ��ϵ�ɵó��綯�ƺ��ڵ��裮
��� �⣺��1����������������ѡ���ʵ������ģ�A������ɵ��һ��
Ϊ�˶���ȷ������ѡ��B��������������0��0.6A��D����ѹ��������0��3V��
������������ֵ��С�����ڵ������ֵ�仯����С����ѡF��������������H�����ء���������
��2���������B��������֪���ʿ��Խ������������ЧΪ��Դ���裬�����Ч����������ʵ�ʵ�Դ���裬�ʲ��ü�ͼ������Ч����ʵ����
��3����U-Iͼ��֪����Դ�ĵ綯��E=1.5V��
��Ч�ڵ���r=$\frac{1.5-1.0}{0.5}$=1.0����
��ʵ������Ϊ1.0-0.2=0.8����
�ʴ�Ϊ����1��BDF����2���ף���3��1.5��0.8
���� ����Ϊ�����ʵ�飬�ڽ���ʱӦע����ȷʵ���ԭ��������Ҫ��ʵ��ԭ����ϱպϵ�·ŷķ���ɵó�����ʽ����ͼ��ó��綯�ƺ��ڵ��裮

��ϰ��ϵ�д�
 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
�����Ŀ
10���繤���ĸ�ѹ��ҵ������ͭ˿��֯�ģ�����˵����ȷ���ǣ�������
| A�� | ͭ˿��֯���·����ױ����ƣ�������ͭ˿��֯ | |
| B�� | ͭ˿����ﵽһ���ĺ�ȣ����ܶ������������� | |
| C�� | �繤��ͭ˿��֯���·���������ʹ���ڵ��Ʊ���Ϊ�㣬�������𱣻����� | |
| D�� | �繤��ͭ˿��֯���·���������ʹ���ڵ糡ǿ�ȱ���Ϊ�㣬�������𱣻����� |
11�� ��ͼ���ס����������ڵ�������ͬһˮƽ�컨���ϣ�����������ͬһˮƽ�߶ȣ�����һ��ϸ��ˮƽ��������ˮƽ�ذ�Ϊ�ο��森ƽ��ʱ���ס�������������ֱ����ļнǷֱ�Ϊ��1�ͦ�2���Ҧ�1����2����ϸ��ͻȻ�Ͽ�������������г�˶���������
��ͼ���ס����������ڵ�������ͬһˮƽ�컨���ϣ�����������ͬһˮƽ�߶ȣ�����һ��ϸ��ˮƽ��������ˮƽ�ذ�Ϊ�ο��森ƽ��ʱ���ס�������������ֱ����ļнǷֱ�Ϊ��1�ͦ�2���Ҧ�1����2����ϸ��ͻȻ�Ͽ�������������г�˶���������
 ��ͼ���ס����������ڵ�������ͬһˮƽ�컨���ϣ�����������ͬһˮƽ�߶ȣ�����һ��ϸ��ˮƽ��������ˮƽ�ذ�Ϊ�ο��森ƽ��ʱ���ס�������������ֱ����ļнǷֱ�Ϊ��1�ͦ�2���Ҧ�1����2����ϸ��ͻȻ�Ͽ�������������г�˶���������
��ͼ���ס����������ڵ�������ͬһˮƽ�컨���ϣ�����������ͬһˮƽ�߶ȣ�����һ��ϸ��ˮƽ��������ˮƽ�ذ�Ϊ�ο��森ƽ��ʱ���ס�������������ֱ����ļнǷֱ�Ϊ��1�ͦ�2���Ҧ�1����2����ϸ��ͻȻ�Ͽ�������������г�˶���������| A�� | �ס������ڵ�������� | B�� | �ס������ڵ������� | ||
| C�� | �Ļ�е��С���ҵĻ�е�� | D�� | ������ٶ�С���ҵ�����ٶ� |
8�� ��ͼ��ʾ��·���ѵ��衢������������������ӵ�ijһ������Դ�ϣ���ʱ��������������I1=I2=I3��������ڵ�·��˵����ȷ���ǣ�������
��ͼ��ʾ��·���ѵ��衢������������������ӵ�ijһ������Դ�ϣ���ʱ��������������I1=I2=I3��������ڵ�·��˵����ȷ���ǣ�������
 ��ͼ��ʾ��·���ѵ��衢������������������ӵ�ijһ������Դ�ϣ���ʱ��������������I1=I2=I3��������ڵ�·��˵����ȷ���ǣ�������
��ͼ��ʾ��·���ѵ��衢������������������ӵ�ijһ������Դ�ϣ���ʱ��������������I1=I2=I3��������ڵ�·��˵����ȷ���ǣ�������| A�� | ��ֻ���������Ƶ�ʣ��������������������� | |
| B�� | ��ֻ��������ĵ�ѹ�������������Ķ��������� | |
| C�� | ����������Դ�ij���Чֵ��ͬ��ֱ����Դ�������������Ķ������� | |
| D�� | ����������Դ�ij���Чֵ��ͬ��ֱ����Դ��I1��I2���䣬I3=0 |
15�� ij�����ٶ�Ϊv0�ļ���ֱ���˶�������ٶ���λ�Ʊ仯��a-xͼ����ͼ��ʾ������о��ȱ���ֱ���˶�λ�Ƶķ�������֪������ͨ��λ��Ϊx0ʱ���ٶȴ�СΪ��������
ij�����ٶ�Ϊv0�ļ���ֱ���˶�������ٶ���λ�Ʊ仯��a-xͼ����ͼ��ʾ������о��ȱ���ֱ���˶�λ�Ƶķ�������֪������ͨ��λ��Ϊx0ʱ���ٶȴ�СΪ��������
 ij�����ٶ�Ϊv0�ļ���ֱ���˶�������ٶ���λ�Ʊ仯��a-xͼ����ͼ��ʾ������о��ȱ���ֱ���˶�λ�Ƶķ�������֪������ͨ��λ��Ϊx0ʱ���ٶȴ�СΪ��������
ij�����ٶ�Ϊv0�ļ���ֱ���˶�������ٶ���λ�Ʊ仯��a-xͼ����ͼ��ʾ������о��ȱ���ֱ���˶�λ�Ƶķ�������֪������ͨ��λ��Ϊx0ʱ���ٶȴ�СΪ��������| A�� | $\sqrt{{v}_{0}^{2}+\frac{1}{2}��{a}_{1}+{a}_{2}��{x}_{0}}$ | B�� | $\sqrt{{v}_{0}^{2}+2��{a}_{1}+{a}_{2}��{x}_{0}}$ | ||
| C�� | $\sqrt{{v}_{0}^{2}+��{a}_{1}+{a}_{2}��{x}_{0}}$ | D�� | $\sqrt{2{v}_{0}^{2}+2��{a}_{1}+{a}_{2}��{x}_{0}}$ |
16��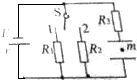 ��ͼ��ʾ����Դ�ĵ綯��ΪE������δ֪��������˫����������1��ʱ���������е�����Ϊm��������Ϊ+q�Ĵ����͵�ǡ�þ�ֹ����������������2��ʱ�����͵��Լ��ٶ�a��ֱ�������ȼ����˶��������е���R1��R2��ȷ���ǣ�������
��ͼ��ʾ����Դ�ĵ綯��ΪE������δ֪��������˫����������1��ʱ���������е�����Ϊm��������Ϊ+q�Ĵ����͵�ǡ�þ�ֹ����������������2��ʱ�����͵��Լ��ٶ�a��ֱ�������ȼ����˶��������е���R1��R2��ȷ���ǣ�������
 ��ͼ��ʾ����Դ�ĵ綯��ΪE������δ֪��������˫����������1��ʱ���������е�����Ϊm��������Ϊ+q�Ĵ����͵�ǡ�þ�ֹ����������������2��ʱ�����͵��Լ��ٶ�a��ֱ�������ȼ����˶��������е���R1��R2��ȷ���ǣ�������
��ͼ��ʾ����Դ�ĵ綯��ΪE������δ֪��������˫����������1��ʱ���������е�����Ϊm��������Ϊ+q�Ĵ����͵�ǡ�þ�ֹ����������������2��ʱ�����͵��Լ��ٶ�a��ֱ�������ȼ����˶��������е���R1��R2��ȷ���ǣ�������| A�� | $\frac{��Eq-ma��dg}{a��Eq-mgd��}$ | B�� | $\frac{[qE-m��g-a��d]g}{��g-a����qE-mgd��}$ | ||
| C�� | $\frac{m��g-a��dg}{��Eq-mgd��}$ | D�� | $\frac{mgdg}{��g-a����Eq-mgd��}$ |
 ��ͼ��ʾ������m=2kg�����徲ֹ��ˮƽ�����ϣ��ܵ���ˮƽ����н�Ϊ��=37�㡢��СF=10N���������ã������ƶ���s=2m������������Ķ�Ħ��������=0.3��gȡ10m/s2����
��ͼ��ʾ������m=2kg�����徲ֹ��ˮƽ�����ϣ��ܵ���ˮƽ����н�Ϊ��=37�㡢��СF=10N���������ã������ƶ���s=2m������������Ķ�Ħ��������=0.3��gȡ10m/s2���� ��ͼ��ʾ�����㹻���Ĺ⻬ˮƽ�����������Сľ��A��B��C�������ֱ�ΪmA��mB��mC����mA=mB=1.0kg��mC=2.0kg������B��C��һ���ᵯ��˩����һ�𣬿�ʼʱ����װ�ô��ھ�ֹ״̬��A��B֮���������ܽ�ըҩ�����������ܽ�ըҩ����ըҩ��ը��������������E=9.0Jת��ΪA��B�Ķ��ܣ���
��ͼ��ʾ�����㹻���Ĺ⻬ˮƽ�����������Сľ��A��B��C�������ֱ�ΪmA��mB��mC����mA=mB=1.0kg��mC=2.0kg������B��C��һ���ᵯ��˩����һ�𣬿�ʼʱ����װ�ô��ھ�ֹ״̬��A��B֮���������ܽ�ըҩ�����������ܽ�ըҩ����ըҩ��ը��������������E=9.0Jת��ΪA��B�Ķ��ܣ���