题目内容
11. 如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,然后由B点水平飞出,AB高度差为h=5m,最后落在BC圆弧上,B与圆心O等高,落点C与O的连线与竖直成θ=30°的夹角,圆弧半径为R=30$\sqrt{3}$m,(g取10m/s2)
如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,然后由B点水平飞出,AB高度差为h=5m,最后落在BC圆弧上,B与圆心O等高,落点C与O的连线与竖直成θ=30°的夹角,圆弧半径为R=30$\sqrt{3}$m,(g取10m/s2)求:(1)运动员从B点飞出时的速度vB的大小
(2)运动员从A滑到B的过程中克服摩擦力所做的功W.
分析 (1)运动员从B到C做平抛运动,运用平抛运动的规律解决问题,其中高度决定时间,通过水平方向运动求出初速度vB.
(2)运动员从A点到B点的过程中克服摩擦力做的功,由于不清楚摩擦力的大小以及A到B得位移,从功的定义式无法求解,所以我们就应该选择动能定理研究.
解答 解:(1)运动员从B到C做平抛运动,根据平抛运动分位移公式,有:
R-Rsin30°=vBt--------①
Rcos30°=$\frac{1}{2}$gt2--------②
又 R=30$\sqrt{3}$m
联立解得:vB=5$\sqrt{3}$m/s---------③
(2)运动员从A到B过程,由动能定理:
mgh-W=$\frac{1}{2}m{v}_{B}^{2}$---------④
解得 W=750J
答:
(1)运动员从B点飞出时的速度vB的大小是5$\sqrt{3}$m/s.
(2)运动员从A滑到B的过程中克服摩擦力所做的功W是750J.
点评 解决平抛运动的问题思路是分解,即研究水平方向的匀速直线运动和竖直方向的自由落体.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.满载A国公民的一航班在飞行途中神秘消失,A国推断航班遭到敌对国家劫持,政府立即调动大量海空军事力量进行搜救,并在第一时间紧急调动了21颗卫星参与搜寻.“调动”卫星的措施之一就是减小卫星环绕地球运动的轨道半径,降低卫星运行的高度,以有利于发现地面(或海洋)目标.下面说法正确的是( )
| A. | 轨道半径减小后,卫星的环绕速度减小 | |
| B. | 轨道半径减小后,卫星的环绕速度增大 | |
| C. | 轨道半径减小后,卫星的环绕周期减小 | |
| D. | 轨道半径减小后,卫星的环绕周期增大 |
2. 在某一高度用细绳提着一质量m=0.2kg的物体,由静止开始沿竖直方向运动过程中物体的机械能与位移关系的E-x图象如图所示,图中两段图线都是直线.取g=10m/s2则下面说法正确的是( )
在某一高度用细绳提着一质量m=0.2kg的物体,由静止开始沿竖直方向运动过程中物体的机械能与位移关系的E-x图象如图所示,图中两段图线都是直线.取g=10m/s2则下面说法正确的是( )
 在某一高度用细绳提着一质量m=0.2kg的物体,由静止开始沿竖直方向运动过程中物体的机械能与位移关系的E-x图象如图所示,图中两段图线都是直线.取g=10m/s2则下面说法正确的是( )
在某一高度用细绳提着一质量m=0.2kg的物体,由静止开始沿竖直方向运动过程中物体的机械能与位移关系的E-x图象如图所示,图中两段图线都是直线.取g=10m/s2则下面说法正确的是( )| A. | 物体在x=2m时的加速度比物体在x=6m时的加速度小 | |
| B. | 物体在x=4m时的速度大小为2$\sqrt{5}$m/s | |
| C. | 物体在0~4m过程中合力故功为10J | |
| D. | 物体在x=2m时的动能可能比物体在x=6m时的动能大 |
19.有一层叠电池,它的电动势E约为9v,内阻r约50Ω,允许输出的最大电流为50mA,为了测定这个电池的电动势和内阻,实验室提供有以下器材可供选择:
(1)为能测多组数据并有较高的准确程度,在虚线方框内画出实验电路原理图,图中各元件要用题目中给出的符号或字母标出.
(2)根据两次实验数据可求出E=$\frac{{U}_{1}{I}_{2}-{U}_{2}{I}_{1}}{{I}_{2}-{I}_{1}}$、r=$\frac{{U}_{1}-{U}_{2}}{21({I}_{2}-{I}_{1})}$(用已知量和测得量的符号表示);式中各符号的意义是U1、U2为电压表示数; I1、I2为电流表示数.

| 器材 | 符号 | 规格 |
| 理想电压表 |  | 测量范围0-15V |
| 电流表 |  | 测量范围0-1mA,内阻r1=100Ω |
| 电流表 |  | 测量范围0-0.6mA,内阻r2=0.01Ω |
| 滑动变阻器 | R | 总电阻约1kΩ |
| 定值电阻 | R0 | 电阻R0=5 |
| 开关(K)一个,导线若干 | ||
(2)根据两次实验数据可求出E=$\frac{{U}_{1}{I}_{2}-{U}_{2}{I}_{1}}{{I}_{2}-{I}_{1}}$、r=$\frac{{U}_{1}-{U}_{2}}{21({I}_{2}-{I}_{1})}$(用已知量和测得量的符号表示);式中各符号的意义是U1、U2为电压表示数; I1、I2为电流表示数.

6.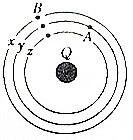 如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )
如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )
 如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )
如图所示,Q为地球,A为空间运行的宇宙飞船,现有一对接舱B在A的后方加速追A,并与A实现对接,y轨道为A的运行轨道,x轨道和z轨道分别是比y轨道高一些和低一些的两个轨道,那么( )| A. | B只有从x轨道开始加速,才有可能实现与A对接 | |
| B. | B只有从y轨道开始加速,才有可能实现与A对接 | |
| C. | B只有从z轨道开始加速,才有可能实现与A对接 | |
| D. | B从x、y轨道开始加速,都有可能实现与A对接,从z轨道开始加速,不能实现与A对接 |
3. 喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
 喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )| A. | 向负极板偏转 | B. | 电势能逐渐减小 | ||
| C. | 运动时间与电场强度大小无关 | D. | 运动轨迹与所带电荷量无关 |

 跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算:
跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算: 某同学利用如图所示的装置探究功与速度变化的关系.
某同学利用如图所示的装置探究功与速度变化的关系.