题目内容
20.蹦床运动是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量为m的运动员,从离水平网面心高h1处自由下落,着网后沿竖直方向蹦回 离水平网面h2高处.已知运动员与网接触的时间为△t,若把这段时间内网对运动员的作用力当作恒力处理,求此力的大小.分析 运动员先做自由落体运动,根据机械能守恒定律求速度;对运动员受力分析,设定正方向,然后根据动量定理列式求解.
解答 解:运动员刚接触网时速度大小,由机械能守恒定律$mg{h_1}=\frac{1}{2}mv_1^2$得
${v_1}=\sqrt{2g{h_1}}$ ①
刚离开网时速度大小,由$mg{h_2}=\frac{1}{2}mv_2^2$得
${v_2}=\sqrt{2g{h_2}}$ ②
设运动员与网接触的过程中网对运动员的作用力为F,取向上为正方向,应用动量定理,
(F-mg)△t=mv2-mv1 ③,
解得:$F=\frac{{m{v_2}+m{v_1}}}{△t}+mg=\frac{{m\sqrt{2g{h_1}}+m\sqrt{2g{h_2}}}}{△t}+mg$
答:此力的大小为$\frac{m\sqrt{2g{h}_{1}}+m\sqrt{2g{h}_{2}}}{△t}+mg$
点评 本题关键是对运动员的各个运动情况分析清楚,然后结合机械能守恒定律、运动学公式、动量定理列式后联立求解即可.

练习册系列答案
相关题目
13.关于磁感线的概念和性质,下列说法中正确的是( )
| A. | 磁感线上各点的切线方向就是各点的磁感应强度的方向 | |
| B. | 磁感线是磁场中客观存在的曲线 | |
| C. | 铁屑在磁场中分布所形成的曲线就是磁感线 | |
| D. | 磁感线总是从磁体N极出发指向磁体的S极 |
11.用起重机将质量相同的物体,从地面匀速提升相同的高度,提升的速率分别为v1和v2,且v1≠v2,那么起重机在两次提升过程中( )
| A. | 速度大的绳的拉力大 | B. | 所需时间相同 | ||
| C. | 功率一样大 | D. | 做的功一样多 |
15.关于两个初速度不为零的匀变速直线运动的合运动,下列说法错误的是( )
| A. | 合速度与合加速度的方向有可能相同 | |
| B. | 合速度与合加速度的方向由可能不相同 | |
| C. | 合运动一定是匀变速直线运动 | |
| D. | 合运动的轨迹可能是直线,也可能是曲线 |
1.物体在以下三个力作用下,可能做匀速直线运动的是( )
| A. | 1 N、6 N、8 N | B. | 3 N、6 N、4 N | C. | 7 N、2 N、6 N | D. | 5 N、9 N、15N |
6. 如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
 如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )| A. | 书对桌面的压力为G | |
| B. | 书对桌面的压力为$\frac{2}{3}$G | |
| C. | 书对桌面有压力是因为桌面产生了向上的形变 | |
| D. | 书对桌面有压力是因为桌面产生了向下的形变 |
 如图所示,A为带正电Q的金属板,沿金属板的垂直平分线,在距板r处放一质量为m、电荷量为q的小球,小球受水平向右的电场力偏转θ角而静止,小球用绝缘丝线悬挂于O点,试求:
如图所示,A为带正电Q的金属板,沿金属板的垂直平分线,在距板r处放一质量为m、电荷量为q的小球,小球受水平向右的电场力偏转θ角而静止,小球用绝缘丝线悬挂于O点,试求: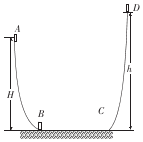 如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接.一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出 C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2.求:
如图所示,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10m,BC长为2m,AB和CD轨道光滑,且均与BC平滑连接.一质量为0.5kg的物体,从A点以6m/s的速度开始运动,经过BC后滑到高出 C点10.8m的D点时其速度为零,已知物体第一次从A点运动到B点的过程中,所用时间为0.8s,取g=10m/s2.求: 如图所示,一个质量m=2.0kg的物体,放在倾角a=37°的斜面上静止不动,现用平行斜面向上、大小为30N的力F使物体开始沿斜面向上匀加速运动,在2s内物体的位移为10m.已知物体与斜面之间的动摩擦因数μ=0.5,斜面足够长,重力加速度g=10m/s2,sin37°=0.6,cos37°=038,求:
如图所示,一个质量m=2.0kg的物体,放在倾角a=37°的斜面上静止不动,现用平行斜面向上、大小为30N的力F使物体开始沿斜面向上匀加速运动,在2s内物体的位移为10m.已知物体与斜面之间的动摩擦因数μ=0.5,斜面足够长,重力加速度g=10m/s2,sin37°=0.6,cos37°=038,求: