题目内容
13.美国科学家在2016年2月11日宣布探测到距离地球13亿光年的两黑洞合并产生的一个时间极短的引力波信号,两个黑洞合并前的质量分别相当于36个和29个太阳质量,假设两黑洞合并前绕它们连线的某一点在万有引力作用下做匀速圆周运动,不计其它天体的影响,则两黑洞合并前做匀速圆周运动时( )| A. | 质量大的黑洞与质量小的黑洞的轨道半径之比为36:29 | |
| B. | 质量大的黑洞与质量小的黑洞的向心加速度大小之比为29:36 | |
| C. | 质量大的黑洞与质量小的黑洞的角速度之比为6:$\sqrt{29}$ | |
| D. | 质量大的黑洞与质量小的黑洞的线速度大小之比为29:36 |
分析 两个黑洞靠相互间的万有引力提供向心力,角速度相等,结合万有引力提供向心力得出两个黑洞的轨道半径之比,根据a=rω2、v=rω得出向心加速度和线速度之比.
解答 解:A、根据$G\frac{{M}_{1}{M}_{2}}{{r}^{2}}={M}_{1}{r}_{1}{ω}^{2}$,$G\frac{{M}_{1}{M}_{2}}{{r}^{2}}={M}_{2}{r}_{2}{ω}^{2}$得,M1r1=M2r2,因为质量大的黑洞和质量小的黑洞质量之比为36:29,则轨道半径之比为29:36,故A错误.
B、根据a=rω2知,因为质量大的黑洞和质量小的黑洞半径之比为29:36,角速度相等,则向心加速度之比为29:36,故B正确,C错误.
D、根据v=rω知,因为质量大的黑洞和质量小的黑洞半径之比为29:36,角速度相等,则线速度之比为29:36,故D正确.
故选:BD.
点评 解决本题的关键知道两个黑洞具有相同的角速度,靠相互间的万有引力提供向心力,向心力大小相等,结合牛顿第二定律和圆周运动的基本知识进行求解,难度不大.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.如图甲所示是一台交流发电机构造示意图,产生交变电流的感应电动势随时间变化的正弦规律如图乙所示.发电机线圈电阻为1Ω,外接电阻为4Ω,其他电阻不计,则( )

| A. | 该交变电流的频率为25Hz | |
| B. | 理想电压表的示数为4V | |
| C. | 在t=0.01s时刻,电路中电流的瞬时值为1A | |
| D. | 若线圈转速变为原来的2倍,将耐压值为5V的电容器与外接电阻并联,该电容器不会被烧坏 |
4.同重力场作用下的物体具有重力势能一样,万有引力场作用下的物体同样具有引力势能,宇宙中有一个质量为M、半径为R的星球,若取无穷远引力势能为零,质量为m的物体距星球球心距离为r时的引力势能为Ep=-G$\frac{Mm}{r}$(G为引力常量),宇航员在该星球上以初速度v0抛出一个物体,不计空气阻力,下列分析正确的是( )
| A. | 若初速度竖直向上,且物体上升高度远小于星球半径,则物体返回到抛出点的时间为$\frac{{R}^{2}{v}_{0}}{GM}$ | |
| B. | 若初速度竖直向上,且物体上升高度大于星球半径,则物体上升的最大高度为$\frac{{R}^{2}{{v}_{0}}^{2}}{2GM}$ | |
| C. | 若初速度沿水平方向,要使物体将不再落回星球表面,则v0≥$\sqrt{\frac{GM}{R}}$ | |
| D. | 若物体能运动到距离星球无穷远处而脱离星球的束缚,则v0≥$\sqrt{\frac{2GM}{R}}$ |
1. 千斤顶是汽车的常备工具.如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为l.0×105N,此时千斤顶两臂间的夹角为120°.则下列判断正确的是( )
千斤顶是汽车的常备工具.如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为l.0×105N,此时千斤顶两臂间的夹角为120°.则下列判断正确的是( )
 千斤顶是汽车的常备工具.如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为l.0×105N,此时千斤顶两臂间的夹角为120°.则下列判断正确的是( )
千斤顶是汽车的常备工具.如图所示是剪式千斤顶,当摇动把手时,螺纹轴就能迫使千斤顶的两臂靠拢,从而将汽车顶起.当车轮刚被顶起时汽车对千斤顶的压力为l.0×105N,此时千斤顶两臂间的夹角为120°.则下列判断正确的是( )| A. | 此时千斤顶对汽乍的支持力为2.0×105N | |
| B. | 此时两臂受到的压力大小均为5.0×104n | |
| C. | 若继续缓慢摇动把手将汽车顶起,螺纹轴的拉力将减小 | |
| D. | 若继续缓慢摇动把手将汽车顶起,两臂受到的压力将增大 |
 某实验小组用下列器材组装如图甲所示简易欧姆表.
某实验小组用下列器材组装如图甲所示简易欧姆表.
 如图所示是探究电磁感应现象的实验装置.用绝缘线将导体AB悬挂在蹄形磁铁的磁场中,闭合开关后,在下面的实验探究中,电流表的指针是否偏转.(选填“偏转”或“不偏转”)
如图所示是探究电磁感应现象的实验装置.用绝缘线将导体AB悬挂在蹄形磁铁的磁场中,闭合开关后,在下面的实验探究中,电流表的指针是否偏转.(选填“偏转”或“不偏转”)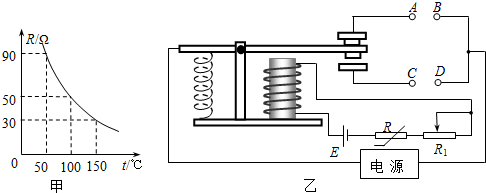

 如图所示,有一四棱镜ABCD,∠B=∠C=90°,∠D=75°.某同学想测量其折射率,他用激光笔从BC面上的P点射入一束激光,从Q点射出时与AD面的夹角为30°,Q点到BC面垂线的垂足为E,P、Q两点到E点的距离分别为a、$\sqrt{3}$a,已知真空中光束为c,求:
如图所示,有一四棱镜ABCD,∠B=∠C=90°,∠D=75°.某同学想测量其折射率,他用激光笔从BC面上的P点射入一束激光,从Q点射出时与AD面的夹角为30°,Q点到BC面垂线的垂足为E,P、Q两点到E点的距离分别为a、$\sqrt{3}$a,已知真空中光束为c,求: