题目内容
1.汽车以10m/s的速度在平直的公路上匀速前进,司机发现正前方x处有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做a=-6m/s2的匀变速运动,若汽车恰好碰不上自行车,则x的大小为( )| A. | 8.33m | B. | 7m | C. | 3.33m | D. | 3m |
分析 根据速度时间公式求出两车速度相等的时间,结合位移关系求出恰好不相撞,开始两车相距的距离.
解答 解:两车速度相等经历的时间t=$\frac{{v}_{1}-{v}_{2}}{a}=\frac{4-10}{-6}s=1s$,
此时汽车的位移${x}_{2}={v}_{2}t+\frac{1}{2}a{t}^{2}=10×1-\frac{1}{2}×6×1m=7m$,自行车的位移x1=v1t=4×1m=4m,
若恰好不相撞,开始相距的距离x=x2-x1=7-4m=3m.
故选:D.
点评 本题考查了运动学中的追及问题,知道速度大者减速追及速度小者,若不相撞,速度相等时,有最小距离,临界情况是速度相等时恰好不相撞.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
6.原来静止的两个物体,它们的质量之比为m1:m2=1:4.当合外力使它们获得相等的动能时,它们速度大小之比v1:v2等于( )
| A. | 1:4 | B. | 4:l | C. | 2:1 | D. | 1:2 |
13.两个放在绝缘架上的相同金属球相距r,球的半径比r小得多,带电量大小分别为q和3q,相互斥力大小为3F.现将这两个金属球相接触,然后分开,仍放回原处,则它们之间的相互作用力大小将变为( )
| A. | 4F | B. | $\frac{4F}{3}$ | C. | 2F | D. | 1.5F |
10. 居住某住宅楼高层的一居民不慎碰落一花盆,花盆在空中依次经过三个完全相同的窗户1、2、3,如图中直线为花盆在空中的运动轨迹,若不计空气阻力的影响,下列说法正确的是( )
居住某住宅楼高层的一居民不慎碰落一花盆,花盆在空中依次经过三个完全相同的窗户1、2、3,如图中直线为花盆在空中的运动轨迹,若不计空气阻力的影响,下列说法正确的是( )
 居住某住宅楼高层的一居民不慎碰落一花盆,花盆在空中依次经过三个完全相同的窗户1、2、3,如图中直线为花盆在空中的运动轨迹,若不计空气阻力的影响,下列说法正确的是( )
居住某住宅楼高层的一居民不慎碰落一花盆,花盆在空中依次经过三个完全相同的窗户1、2、3,如图中直线为花盆在空中的运动轨迹,若不计空气阻力的影响,下列说法正确的是( )| A. | 花盆通过第3个窗户所用的时间最长 | |
| B. | 花盆通过第1个窗户所用的时间最长 | |
| C. | 花盆通过第3个窗户的平均速度最小 | |
| D. | 花盆通过第1个窗户的平均速度最小 |
 如图所示,一条小河两岸的高度差h=5m,一辆长1.5m的摩托车以v0=20m/s的水平速度向河对岸飞出,摩托车后轮恰好越过小河.若飞行中不计空气阻力,取当地的重力加速度g=10m/s2.试求:
如图所示,一条小河两岸的高度差h=5m,一辆长1.5m的摩托车以v0=20m/s的水平速度向河对岸飞出,摩托车后轮恰好越过小河.若飞行中不计空气阻力,取当地的重力加速度g=10m/s2.试求: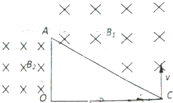 有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求:
有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求:
 如图所示,导线框abcdef的质量为m,电阻为r,ab边长为l1,cd边长$\frac{l_1}{3}$,bc、de边长均为l2,ab边正下方h处有单边有界匀强磁场区域,其水平边界为PQ,磁感应强度为B,方向垂直于纸面向里.使线框从静止开始下落,下落过程中ab边始终水平,且cd边进入磁场前的某一时刻,线框已开始匀速运动.重力加速度为g,不计空气阻力.求:
如图所示,导线框abcdef的质量为m,电阻为r,ab边长为l1,cd边长$\frac{l_1}{3}$,bc、de边长均为l2,ab边正下方h处有单边有界匀强磁场区域,其水平边界为PQ,磁感应强度为B,方向垂直于纸面向里.使线框从静止开始下落,下落过程中ab边始终水平,且cd边进入磁场前的某一时刻,线框已开始匀速运动.重力加速度为g,不计空气阻力.求: 如图所示,质量为m、电荷量为e的粒子从A点以v0的速度垂直电场线沿直线AO方向射入匀强电场,由B点飞出电场时速度方向与AO方向成45°,已知AO的水平距离为d,不计重力.求:
如图所示,质量为m、电荷量为e的粒子从A点以v0的速度垂直电场线沿直线AO方向射入匀强电场,由B点飞出电场时速度方向与AO方向成45°,已知AO的水平距离为d,不计重力.求: