题目内容
11. 如图所示,质量为m、电荷量为e的粒子从A点以v0的速度垂直电场线沿直线AO方向射入匀强电场,由B点飞出电场时速度方向与AO方向成45°,已知AO的水平距离为d,不计重力.求:
如图所示,质量为m、电荷量为e的粒子从A点以v0的速度垂直电场线沿直线AO方向射入匀强电场,由B点飞出电场时速度方向与AO方向成45°,已知AO的水平距离为d,不计重力.求:(1)从A点到B点所用的时间;
(2)粒子在B点的速度大小;
(3)匀强电场的电场强度大小.
分析 (1)粒子从A点以v0的速度沿垂直电场线方向射入电场,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由水平距离d和初速度v0可求出时间.
(2)将粒子射出电场的速度进行分解,求出在B点的速度;
(3)将粒子射出电场的速度进行分解,求出竖直方向分速度vy,由牛顿第二定律和vy=at结合求出电场强度E.
解答 解:(1)粒子从A点以v0的速度沿垂直电场线方向射入电场,水平方向做匀速直线运动,则有:
t=$\frac{d}{{v}_{0}}$
(2)由B点飞出电场时速度方向与AO方向成45°,则粒子在B点的速度大小v=$\sqrt{2}{v}_{0}$,
(3)根据牛顿第二定律得:
a=$\frac{qE}{m}$
将粒子射出电场的速度v进行分解,则有 vy=v0tan45°=v0,又vy=at,得:
v0=$\frac{qE}{m}•\frac{d}{{v}_{0}}=\frac{eEd}{m{v}_{0}}$,解得:
E=$\frac{m{v}_{0}^{2}}{ed}$
答:(1)从A点到B点所用的时间为$\frac{d}{{v}_{0}}$;
(2)粒子在B点的速度大小为$\sqrt{2}{v}_{0}$;
(3)匀强电场的电场强度大小为$\frac{m{v}_{0}^{2}}{ed}$.
点评 本题运用运动的分解法研究类平抛运动,关键将速度进行分解,由牛顿第二定律和运动学公式相结合进行研究,不难.

练习册系列答案
相关题目
1.汽车以10m/s的速度在平直的公路上匀速前进,司机发现正前方x处有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做a=-6m/s2的匀变速运动,若汽车恰好碰不上自行车,则x的大小为( )
| A. | 8.33m | B. | 7m | C. | 3.33m | D. | 3m |
2.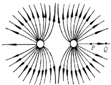 如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )
如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )
 如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )
如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )| A. | 图示为单个正点电荷的电场线 | B. | 图示为等量异种点电荷的电场线 | ||
| C. | EP>EQ | D. | φP<φQ |
6.一质子以速度v穿过互相垂直的电场和磁场区域而没有发生偏转,不考虑重力的影响,则( )


| A. | 若电子以相同速度v射入该区域,将会发生偏转 | |
| B. | 无论何种带电粒子,只要以相同的速度v射入都不会发生偏转 | |
| C. | 若质子的速度v′<v,它将向上偏转 | |
| D. | 若质子的速度v′>v,它将向上偏转 |
16.亚里士多德认为:物体越重下落得越快.伽利略否定了这种看法.在同一高塔顶端同时释放一片羽毛和一个金属球,金属球先于羽毛落到地面,根据伽利略的观点这主要是因为( )
| A. | 它们的重量不同 | B. | 它们的密度不同 | ||
| C. | 它们的材料不同 | D. | 它们受到的空气阻力影响不同 |
3. 如图所示,a、b两根垂直纸面的直导线通有等值的电流,两导线旁有一点P,P点到a、b距离相等,关于P点的磁场方向,以下判断正确的是( )
如图所示,a、b两根垂直纸面的直导线通有等值的电流,两导线旁有一点P,P点到a、b距离相等,关于P点的磁场方向,以下判断正确的是( )
 如图所示,a、b两根垂直纸面的直导线通有等值的电流,两导线旁有一点P,P点到a、b距离相等,关于P点的磁场方向,以下判断正确的是( )
如图所示,a、b两根垂直纸面的直导线通有等值的电流,两导线旁有一点P,P点到a、b距离相等,关于P点的磁场方向,以下判断正确的是( )| A. | a中电流方向向纸外,b中电流方向向纸里,则P点的磁场方向向右 | |
| B. | a中电流方向向纸外,b中电流方向向纸里,则P点的磁场方向向左 | |
| C. | a中电流方向向纸里,b中电流方向向纸外,则P点的磁场方向向右 | |
| D. | a中电流方向向纸外,b中电流方向向纸外,则P点的磁场方向向左 |
20. 在如图所示电路中,闭关开关S,当滑动变阻器的滑动触头P向下滑动时,三个理想电表的示数都发生了变化,电表的示数分别用I、U1、U2表示,下列判断正确的是( )
在如图所示电路中,闭关开关S,当滑动变阻器的滑动触头P向下滑动时,三个理想电表的示数都发生了变化,电表的示数分别用I、U1、U2表示,下列判断正确的是( )
 在如图所示电路中,闭关开关S,当滑动变阻器的滑动触头P向下滑动时,三个理想电表的示数都发生了变化,电表的示数分别用I、U1、U2表示,下列判断正确的是( )
在如图所示电路中,闭关开关S,当滑动变阻器的滑动触头P向下滑动时,三个理想电表的示数都发生了变化,电表的示数分别用I、U1、U2表示,下列判断正确的是( )| A. | I减小,U1增大,U2增大 | B. | I减小,U1减小,U2增大 | ||
| C. | I增大,U1增大,U2减小 | D. | I增大,U1减小,U2减小 |
1.真空中有两个静止的点电荷,它们之间的作用力为 F,若它们的带电量都增大为原来的2倍,它们之间的相互作用力变为( )
| A. | 16F | B. | 4F | C. | F | D. | $\frac{F}{2}$ |
