题目内容
1. 如图所示,A,B是竖直放置的平行金属板,B中间有一小孔,水平放置的M,N两平行金属板相距d=0.50m,板长L=1m,两板间有电压U2=150V紧靠平行板右侧边缘的xOy直角坐标系以N板右端为原点,在xOy坐标系的第一象限内有垂直纸面向外的匀强磁场,磁感应强度的大小B=$\frac{8\sqrt{3}}{3}$×10-2T,磁场边界OC与x轴夹角∠COx=60°,现有比荷$\frac{q}{m}$=$\sqrt{3}×$106C/kg的带正电粒子(重力不计),通过AB板间的加速电压U1;加速后沿靠近M板的水平方向进入偏转电场,带电粒子离开偏转电场后垂直于OC边界进入匀强磁场区域,求:
如图所示,A,B是竖直放置的平行金属板,B中间有一小孔,水平放置的M,N两平行金属板相距d=0.50m,板长L=1m,两板间有电压U2=150V紧靠平行板右侧边缘的xOy直角坐标系以N板右端为原点,在xOy坐标系的第一象限内有垂直纸面向外的匀强磁场,磁感应强度的大小B=$\frac{8\sqrt{3}}{3}$×10-2T,磁场边界OC与x轴夹角∠COx=60°,现有比荷$\frac{q}{m}$=$\sqrt{3}×$106C/kg的带正电粒子(重力不计),通过AB板间的加速电压U1;加速后沿靠近M板的水平方向进入偏转电场,带电粒子离开偏转电场后垂直于OC边界进入匀强磁场区域,求:(1)加速电压U1的大小,
(2)带电粒子进入磁场时离O点的距离
(3)带电粒子从离开电场到离开磁场的总时间.
分析 (1)带电粒子在电场中做类平抛运动,由类平抛运动规律可言求出粒子的初速度.根据动能定理求出加速电压的大小.
(2)根据竖直方向上偏转位移,结合几何关系求出带电粒子进入磁场时离O点的距离.
(3)求出粒子在离开电场到进入磁场的时间,求出粒子在匀强磁场中的运动时间,最后求出总的运动时间.
解答  解:(1)粒子运动轨迹如图所示:
解:(1)粒子运动轨迹如图所示:
带电粒子在电场中做类平抛运动,
粒子垂直射入磁场,则速度偏向角为30°,
粒子离开磁场时的竖直分速度:vy=at=$\frac{q{U}_{2}}{md}•\frac{l}{{v}_{0}}$,
竖直分速度与水平分速度之比:$\frac{{v}_{y}}{{v}_{0}}=tan30°$,
代入数据解得:${v}_{0}=3×1{0}^{4}m/s$,
根据$q{U}_{1}=\frac{1}{2}m{{v}_{0}}^{2}$得:${U}_{1}=\frac{m{{v}_{0}}^{2}}{2q}=\frac{9×1{0}^{8}}{2×\sqrt{3}×1{0}^{6}}$=$150\sqrt{3}V$.
(2)粒子在电场中的偏转位移为:$y=\frac{1}{2}a{t}^{2}=\frac{1}{2}\frac{q{U}_{2}}{md}\frac{{l}^{2}}{{{v}_{0}}^{2}}$,
代入数据解得:y=$\frac{\sqrt{3}}{6}m$,
根据几何关系得,带电粒子进入磁场时离O点的距离为:
s1=$(d-y)cos30°=(0.5-\frac{\sqrt{3}}{6})×\frac{\sqrt{3}}{2}$m=$\frac{\sqrt{3}-1}{4}$m.
(3)粒子离开电场的速度为:
v=$\frac{{v}_{0}}{cos30°}=\frac{3×1{0}^{4}}{\frac{\sqrt{3}}{2}}m/s=2\sqrt{3}×1{0}^{4}m/s$,
粒子离开电场后做匀速直线运动,直线运动距离:
s2=(d-y)sin30°,
代入数据解得:s2=$\frac{3-\sqrt{3}}{12}m$,
则运动时间为:${t}_{1}=\frac{{s}_{2}}{v}$,
代入数据解得:${t}_{1}=\frac{\sqrt{3}-1}{24}×1{0}^{-4}s$,
粒子进入磁场后的轨道半径为R,R=$\frac{mv}{qB}$,
代入数据解得:R=$\frac{\sqrt{3}}{4}m$,
因为${s}_{1}=\frac{\sqrt{3}-1}{4}m$,
由正弦定理得:$\frac{R}{sin120°}=\frac{R-{s}_{1}}{sinθ}$,
解得θ=30°,
由此可知,带电粒子在磁场中的偏转角度为30°,
由在磁场中的运动时间为:t2=$\frac{1}{12}T=\frac{1}{12}×\frac{2πm}{qB}$
代入数据解得:t2=$\frac{π}{48}×1{0}^{-4}s$
则总运动时间为:t=t1+t2=$(\frac{\sqrt{3}-1}{24}+\frac{π}{48})×1{0}^{-4}s$.
答:(1)加速电压U1的大小为$150\sqrt{3}$V.
(2)带电粒子进入磁场时离O点的距离为$\frac{\sqrt{3}-1}{4}$m.
(3)带电粒子从离开电场到离开磁场的总时间为$(\frac{\sqrt{3}-1}{24}+\frac{π}{48})×1{0}^{-4}s$..
点评 考查带电粒子做匀速圆周运动与类平抛运动中,用牛顿第二定律与运动学公式,并结合几何关系来处理这两种运动,强调运动的分解,并突出准确的运动轨迹图.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案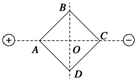 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )| A. | A点的电场强度等于B点的电场强度 | |
| B. | B、D两点的电场强度及电势均相同 | |
| C. | 一电子由B点沿B→C→D路径移至D点,电势能先减小后增大 | |
| D. | 一电子由C点沿C→O→A路径移至A点,电场力对其先做负功后做正功 |
 如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )
如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )| A. | C,D两点的电场强度不同,电势相同 | |
| B. | C,D两点的电场强度相同,电势不同 | |
| C. | 将一正电荷从C点移到D点,电场力对该正电荷先做正功,然后做负功 | |
| D. | 将一正电荷从C点移到D点,电场力对该正电荷先做负功,然后做正功 |
 如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )
如图,固定有滑圆弧轨道的小车A静止在光的水平面上,轨道足够长,其下部分水平,有一小滑块B以某水平初速度滑上小车,滑轮不从圆弧上端滑出,则滑块B在车上运动的过程中( )| A. | 当滑块上升到最大高度时,滑块的速度为零 | |
| B. | 滑块运动过程中机械能守恒 | |
| C. | 滑块离开小车时的速度与滑上小车时的速度大小相等 | |
| D. | 滑块B在小车上运动的过程中,滑块与小车组成的系统动量不守恒 |
 一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出:
一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出:

 2010年10月1日下午嫦娥二号由“长征三号丙”运载火箭发射升空,经中途修正,在近月点自主实施制动,实现月球捕获,变轨后进入100公里环月圆轨道Ⅰ.在环月运行期间,卫星将择机实施轨道机动,进入100公里×15公里的椭圆轨道Ⅱ,开展技术验证和二期工程备选着陆区成像试验.(如图)M、N分别为轨道Ⅱ上的点,P为轨道Ⅰ上的点,V1、V2、V3为卫星在对应点的速度,a1、a2、a3为在对应点的加速度,则( )
2010年10月1日下午嫦娥二号由“长征三号丙”运载火箭发射升空,经中途修正,在近月点自主实施制动,实现月球捕获,变轨后进入100公里环月圆轨道Ⅰ.在环月运行期间,卫星将择机实施轨道机动,进入100公里×15公里的椭圆轨道Ⅱ,开展技术验证和二期工程备选着陆区成像试验.(如图)M、N分别为轨道Ⅱ上的点,P为轨道Ⅰ上的点,V1、V2、V3为卫星在对应点的速度,a1、a2、a3为在对应点的加速度,则( )