题目内容
10.从离地面125m的空中自由落下一个小球,取g=10m/s2,求小球:(1)经过多长时间落到地面?
(2)自开始下落计时,在第1s内的位移及最后l s内的位移.
(3)若该小球是从高楼楼顶屋檐自由下落,在△t=0.25s内通过高度为△h=2m的窗口,求窗口的顶端距高楼楼顶屋檐多高?
分析 (1)由题意可知,小球做自由落体运动,由自由落体规律$h=\frac{1}{2}g{t}^{2}$可得落地时间.
(2)由$h=\frac{1}{2}g{t}^{2}$可得第1s内的位移,求出下落t-1s内的位移,即可求得最后1s的位移
(3)设下落点距窗户上缘的距离为h′,根据自由落体运动位移时间公式即可解题.
解答 解:(1)物体自由下落,故初速度为零,做自由落体运动,取竖直向下为正方向,小球做自由落体运动,由$h=\frac{1}{2}g{t}^{2}$,得落地时间:
$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×125}{10}}s=5s$.
(2)第1s内的位移:${h}_{1}=\frac{1}{2}{gt}_{1}^{2}=\frac{1}{2}×10×{1}^{2}m=5m$
前4s位移为${h}_{4}=\frac{1}{2}{gt}_{4}^{2}=\frac{1}{2}×10×{4}^{2}m=80m$
最后l s内的位移h5=h-h4=45m
(3)设小球自由下落到窗顶的位移为h,所用时间为t′,窗高为△h′,则
h′=$\frac{1}{2}gt{′}^{2}$
$h′+△h′=\frac{1}{2}g(t′+△t)^{2}$
其中△h=2m,△t=0.25s代入数据解得:
h=2.28m
答:(1)经过5s时间落到地面
(2)自开始下落计时,在第1s内的位移及最后l s内的位移分别为5m,45m.
(3)若该小球是从高楼楼顶屋檐自由下落,在△t=0.25s内通过高度为△h=2m的窗口,窗口的顶端距高楼楼顶屋檐高为2.28m
点评 掌握自由落体的特征:初速度为零,只受重力,加速度为g,由此来应用相关的规律,记忆相关的公式都比较便捷;另外要会区分时间和时刻

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案 如图所示,一根轻质弹簧,放在光滑的水平面上,左端固定在竖直墙壁上,当用8N的力水平向右拉弹簧右端时,弹簧的伸长量为4cm;当用12N的力水平向左压弹簧右端时,弹簧的压缩量为(设上述两种情况中弹簧的形变均为弹性形变)( )
如图所示,一根轻质弹簧,放在光滑的水平面上,左端固定在竖直墙壁上,当用8N的力水平向右拉弹簧右端时,弹簧的伸长量为4cm;当用12N的力水平向左压弹簧右端时,弹簧的压缩量为(设上述两种情况中弹簧的形变均为弹性形变)( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 4cm |
 一个质量为50kg的人,站在竖直向上运动着的升降机地板上,他看到升降机内挂着重物的弹簧秤的示数为40N.已知弹簧秤下挂着的物体的重力为50N,取g=10m/s2,以下说法正确的是( )
一个质量为50kg的人,站在竖直向上运动着的升降机地板上,他看到升降机内挂着重物的弹簧秤的示数为40N.已知弹簧秤下挂着的物体的重力为50N,取g=10m/s2,以下说法正确的是( )| A. | 地板对人的支持力为600N | B. | 地板对人的支持力为400N | ||
| C. | 人的重力小于500N | D. | 人处于失重状态 |
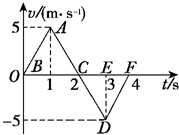
| A. | t=1s时离原点最远 | B. | t=2s时离原点最远 | ||
| C. | t=3s时回到原点 | D. | t=4s时回到原点,路程为20m |
| A. | 物体的速度为零,则加速度也为零 | |
| B. | 物体的速度变化越大,则加速度越大 | |
| C. | 物体的速度变化越快,则加速度越大 | |
| D. | 物体加速度的大小与速度变化快慢无关 |
| A. | 开普勒的研究成果 | |
| B. | 卡文迪许通过扭秤试验试验得出的引力常数 | |
| C. | 牛顿第二定律 | |
| D. | 牛顿第三定律 |
 如图所示,圆形区域内有垂直纸面的匀强电场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动估计如图所示,若带点粒子只受磁场力的作用,则下列说法中正确的是( )
如图所示,圆形区域内有垂直纸面的匀强电场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动估计如图所示,若带点粒子只受磁场力的作用,则下列说法中正确的是( )| A. | a粒子动能最大 | B. | c粒子速率最大 | ||
| C. | c粒子在磁场中运动的时间最长 | D. | 它们做圆周运动的周期Ta=Tb=Tc |
