题目内容
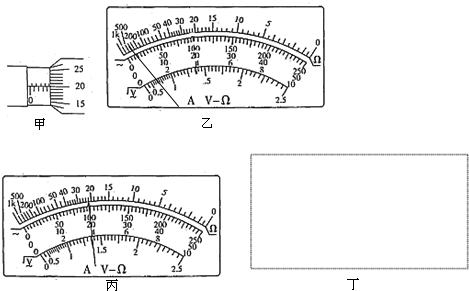
14. 某同学用下列器材组装的简易欧姆表,如图所示.
某同学用下列器材组装的简易欧姆表,如图所示.a、干电池一节:电动势为1.5V且其内电阻可忽略;
b、电流计一块:量程为0至1mA,最小刻度0.1mA,内电阻20Ω;
c、可变电阻一只:阻值范围为100Ω至2500Ω.
(1)测量电阻前,先进行欧姆调零.将可变电阻P的阻值调节为R=1480,此时电流计指针指到最大刻度;
(2)欧姆表正确调零后,将待测电阻的两端分别连至红、黑表笔,若电流计的示数为0.5mA,待测电阻的阻值Rx=1500;
(3)若将电流计示数范围限制在0.1mA到0.9mA之间,欧姆表可量测的电阻范围为167Ω~13500Ω.;
(4)如果将r=20Ω的电阻与电流计并联,重新调零后,与第(3)问相比,可测见的电阻范围将如何变化?
可测量的电阻范围将变小.
分析 (1)(2)由全电路欧姆定律可求得电阻阻值.
(3)将电流值代入全电路欧姆定律可求得其阻值范围.
(4)电阻与电流计并联后,调零时,通过电流计的最大电流为1 mA,通过干路的电流为2mA,确定其阻值.
解答 解:(1)电流计的读数为1 mA时,全电路的电阻为$\frac{1.5V}{1×1{0}^{-3}A}$=1500A.
所以,可变电阻的阻值为1500Ω-20Ω=1480Ω.
(2)调零后,可变电阻的阻值为1480Ω,电流计的示数为0.5 mA时,待测电阻的阻值为$\frac{1.5V}{0.5×1{0}^{-3}A}$-1480Ω-20Ω=1500Ω(即欧姆表内阻等于中值电阻)
(3)电流计示数0.1 mA,待测电阻的阻值为$\frac{1.5V}{0.1×1{0}^{-3}A}$-1480Ω-20Ω=1350Ω;
电流计示数0.9 mA,待测电阻的阻值为$\frac{1.5V}{0.9×1{0}^{-3}A}$-1480Ω-20Ω≈167Ω.
欧姆表可量测的电阻范围167Ω~13500Ω.
(4)可测量的电阻范围将变小,因电流计两端并联与电流计内阻相同的电阻后,电路中的总电流变为原来的两倍,而电池的电动势仍为1.5V,故可测量的电阻范围将变小.
或者:电阻与电流计并联后,调零时,通过电流计的最大电流为1 mA,通过干路的电流为2mA,全电路的电阻为$\frac{1.5V}{2×1{0}^{-3}A}$=750Ω.
所以,可变电阻的阻值为750Ω-10Ω=740Ω.
电流计示数0.1 mA,待测电阻的阻值为$\frac{1.5V}{0.2×1{0}^{-3}A}$-740Ω-10Ω=6750Ω,
电流计示数0.9 mA,待测电阻的阻值为$\frac{1.5V}{1.8×1{0}^{-3}A}$-740Ω-10Ω≈83Ω,
欧姆表可量测的电阻范围83Ω~6750Ω.
答:(1)1480Ω
(2)1500Ω
(3)167Ω~13500Ω
(4)可测量的电阻范围将变小或者83Ω~67500Ω
点评 考查欧姆表的原理为闭合电路欧姆定律,明确使用欧姆表测电阻时要选择合适的档位,指针要指在刻度盘中央刻度附近;对电表读数时,要先确定其量程与分度值,然后再读数,读数时视线要与电表刻度线垂直.

 如图所示,轻质细绳AO和BO相交于O点,其A、B端是固定的,在O点悬挂质量为m的物体,平衡时,AO呈水平,BO与水平面夹角为θ,已知细绳AO和BO能承受的最大拉力相同,AO和BO的拉力大小分别为F1和F2.则( )
如图所示,轻质细绳AO和BO相交于O点,其A、B端是固定的,在O点悬挂质量为m的物体,平衡时,AO呈水平,BO与水平面夹角为θ,已知细绳AO和BO能承受的最大拉力相同,AO和BO的拉力大小分别为F1和F2.则( )| A. | F1=mg tanθ | |
| B. | F2=$\frac{mg}{cosθ}$ | |
| C. | F1与F2的合力大小为mg,方向竖直向上 | |
| D. | 增大物体的质量,最先断的是细绳AO |
 磁流体发电机可简化为如下模型:两块长、宽分别为a、b的平行板,彼此相距L,板间通入已电离的速度为v的气流,两板间存在一磁感应强度大小为B的磁场,磁场方向与两板平行,并与气流垂直,如图所示.把两板与外电阻R连接起来,在磁场力作用下,气流中的正、负离子分别向两板移动形成电流.设该气流的导电率(电阻率的倒数)为σ,则( )
磁流体发电机可简化为如下模型:两块长、宽分别为a、b的平行板,彼此相距L,板间通入已电离的速度为v的气流,两板间存在一磁感应强度大小为B的磁场,磁场方向与两板平行,并与气流垂直,如图所示.把两板与外电阻R连接起来,在磁场力作用下,气流中的正、负离子分别向两板移动形成电流.设该气流的导电率(电阻率的倒数)为σ,则( )| A. | 该磁流体发电机模型的内阻为r=$\frac{L}{σab}$ | |
| B. | 产生的感应电动势为E=Bav | |
| C. | 流过外电阻R的电流强度I=$\frac{BLv}{R+\frac{L}{σab}}$ | |
| D. | 该磁流体发电机模型的路端电压为$\frac{BLvR}{R+σ\frac{L}{ab}}$ |
 A和B两物体在同一直线上运动的v-t图线如图,已知在第3s末两个物体相遇,则此过程中两物相同的是( )
A和B两物体在同一直线上运动的v-t图线如图,已知在第3s末两个物体相遇,则此过程中两物相同的是( )| A. | 加速度 | B. | 出发地 | C. | 速度方向 | D. | 合外力 |

 如图所示,墙角固定着一根轻质弹簧,质量为m的物块与弹簧接触并对弹簧压缩,弹簧此时的弹性势能为Ep.质量为M=2m的$\frac{1}{4}$光滑圆弧形滑槽静止在光滑水平面上,滑槽底端与水平面相切.现释放弹簧,重力加速度为g,求
如图所示,墙角固定着一根轻质弹簧,质量为m的物块与弹簧接触并对弹簧压缩,弹簧此时的弹性势能为Ep.质量为M=2m的$\frac{1}{4}$光滑圆弧形滑槽静止在光滑水平面上,滑槽底端与水平面相切.现释放弹簧,重力加速度为g,求 如图所示,两个壁厚可忽略的圆柱形金属筒A和B套在一起,底部到顶部的高度为18cm,两者横截面积相等,光滑接触且不漏气.将A用绳系于天花板上,用一块绝热板托住B,使它们内部密封的气体压强与外界大气压相同,均为1.0×105Pa,然后缓慢松开绝热板,让B下沉,当B下沉了2cm时,停止下沉并处于静止状态.求:
如图所示,两个壁厚可忽略的圆柱形金属筒A和B套在一起,底部到顶部的高度为18cm,两者横截面积相等,光滑接触且不漏气.将A用绳系于天花板上,用一块绝热板托住B,使它们内部密封的气体压强与外界大气压相同,均为1.0×105Pa,然后缓慢松开绝热板,让B下沉,当B下沉了2cm时,停止下沉并处于静止状态.求: