题目内容
15. 平板小车C放在光滑水平面上,现有质量为2m的物块A和质量为m的木块B,分别以2v0和v0的初速度沿同一直线从小车的两端水平相向滑上小车,如图所示,设A、B两物块与小车的动摩擦因数分别为μ和2μ,小车的质量为3m,A、B均可视为质点.
平板小车C放在光滑水平面上,现有质量为2m的物块A和质量为m的木块B,分别以2v0和v0的初速度沿同一直线从小车的两端水平相向滑上小车,如图所示,设A、B两物块与小车的动摩擦因数分别为μ和2μ,小车的质量为3m,A、B均可视为质点.(1)在A、B物块同时相对小车滑动过程中,简要分析小车的运动状态.
(2)为使A、B两物块不相碰,平板小车至少要多长?
分析 (1)对小车受力分析,进而判断小车的运动情况;
(2)要想使物体A、B不相碰,A、B相对于小车的位移大小之和等于车的长度,对三个物体组成的系统,应用动量守恒定律以及能量守恒定律结合运动学基本公式求出小车的长度.
解答 解:(1)因A、B物块在滑动过程中,对小车的摩擦力大小相等、方向相反,所以小车C不动.
(2)A、B物块在滑动过程中,小车C不动,AB组成的系统受到的合外力为零,系统动量守恒,当B停止运动时,设A的速度为vA,以向右为正,根据动量守恒定律,得
2m•2v0-mv0=2mvA
解得:${v}_{A}=\frac{3}{2}{v}_{0}$
在这段时间内,A、B的加速度分别为${a}_{A}=\frac{μ•2mg}{2m}=μg$,${a}_{B}=\frac{μ•2mg}{m}=2μg$,
在这段时间内A、B在车上滑行的距离为 ${x}_{A}=\frac{(2{v}_{0})^{2}-{{v}_{A}}^{2}}{2{a}_{A}}=\frac{7{{v}_{0}}^{2}}{8μg}$,${x}_{B}=\frac{{{v}_{0}}^{2}}{2{a}_{B}}=\frac{{{v}_{0}}^{2}}{4μg}$,
此后A相对小车仍在运动,A对车的摩擦力使车和B一同向右加速运动,直接三者速度相等,A、B恰好接触,此时小车的长度为最小长度.设共同速度为v′,则有
2m•2v0-mv0=(2m+m+3m)v′
$μ•2mg{x}_{3}=\frac{1}{2}×2m{{v}_{A}}^{2}-\frac{1}{2}×6mv{′}^{2}$
解得:${x}_{3}=\frac{{{3v}_{0}}^{2}}{4μg}$
则车的长度至少为L=${x}_{A}+{x}_{B}+{x}_{3}=\frac{{{15v}_{0}}^{2}}{8μg}$
答:(1)在A、B物块同时相对小车滑动过程中,小车C不动.
(2)为使A、B两物块不相碰,平板小车的长度至少为$\frac{{{15v}_{0}}^{2}}{8μg}$.
点评 熟练应用动量守恒定律、能量守恒定律是正确解题的关键,解题时要分析清楚运动过程,注意应用动量守恒定律解题时要规定正方向.

 名校课堂系列答案
名校课堂系列答案| A. | B=0.04T | B. | B=4T | C. | B≤4T | D. | B≥4T |

| A. | 甲质点在0-1s内做匀速直线运动 | B. | 甲质点在3s内通过的位移为1m | ||
| C. | 乙质点作往返运动 | D. | 乙质点的加速度不变 |

| A. | 使导线中电流增强 | B. | 使导线中电流减弱 | ||
| C. | 使线框靠近导线移动 | D. | 使线框远离导线移动 |
| A. | 2:6:5 | B. | 2:8:7 | C. | 1:1:7 | D. | 4:12:9 |

 多用电表是一种测量电学量的多功能、多量程的测量仪表.
多用电表是一种测量电学量的多功能、多量程的测量仪表.
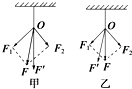 在“探究求合力的方法”实验中,
在“探究求合力的方法”实验中,