题目内容
5.甲、乙两物体在光滑水平地面上沿一直线相向而行,甲质量为6kg,速度大小为8m/s,乙质量为4kg,速度大小为6m/s,它们的总动量大小为24kgm/s.两者碰撞后,甲沿原方向运动,速度大小为2m/s,则乙的速度大小为3m/s.分析 取甲物体的速度方向为正方向,分别表示出两物体的动量,即可求出总动量.碰撞过程遵守动量守恒,求出乙物体的速度大小.
解答 解:取甲物体的速度方向为正方向,
甲乙的总动量大小为P=m甲v甲-m乙v乙=6×8-4×6=24(kgm/s).
根据动量守恒得
P=m甲v甲′+m乙v乙′,
解得,v乙′=3m/s
故答案为:24;3
点评 对于碰撞的基本规律是动量守恒,注意规定正方向列出守恒等式,难度不大,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
15.钢球A自塔顶自由落下2m时,钢球B自离塔顶6m距离处自由落下,两钢球同时到达地面,不计空气阻力,则塔高为( )
| A. | 24m | B. | 16m | C. | 12m | D. | 8m |
16. 质量均为m的两个小球A、B固定在轻质等腰直角形框架的两个顶点上,框架可绕过O点的光滑转轴在竖直平面内自由转动,两直角边长为L.开始时,OB边水平,OA边竖直,现由静止释放,重力加速度为g,忽略空气阻力.下列说法中正确的是( )
质量均为m的两个小球A、B固定在轻质等腰直角形框架的两个顶点上,框架可绕过O点的光滑转轴在竖直平面内自由转动,两直角边长为L.开始时,OB边水平,OA边竖直,现由静止释放,重力加速度为g,忽略空气阻力.下列说法中正确的是( )
 质量均为m的两个小球A、B固定在轻质等腰直角形框架的两个顶点上,框架可绕过O点的光滑转轴在竖直平面内自由转动,两直角边长为L.开始时,OB边水平,OA边竖直,现由静止释放,重力加速度为g,忽略空气阻力.下列说法中正确的是( )
质量均为m的两个小球A、B固定在轻质等腰直角形框架的两个顶点上,框架可绕过O点的光滑转轴在竖直平面内自由转动,两直角边长为L.开始时,OB边水平,OA边竖直,现由静止释放,重力加速度为g,忽略空气阻力.下列说法中正确的是( )| A. | 框架转动过程中地球、球A、球B框架构成的系统机械能守恒 | |
| B. | 释放后,当OB杆转到与水平发那个向成45°时,两球速度达到最大 | |
| C. | 框架转动过程中B球不能到达A球初始位置 | |
| D. | 框架转动过程中两球达到的最大速度为$\sqrt{(\sqrt{2}-1)gl}$ |
13.在杨氏双缝实验中,若两缝之间的距离稍为加大,其他条件不变,则干涉条纹将( )
| A. | 变密 | B. | 变疏 | C. | 不变 | D. | 消失 |
20. 如图,两列水波波源S1和S2的振幅分别为2A和A,某时刻它们形成的波峰和波谷分别由实线和虚线表示.下列说法正确的是( )
如图,两列水波波源S1和S2的振幅分别为2A和A,某时刻它们形成的波峰和波谷分别由实线和虚线表示.下列说法正确的是( )
 如图,两列水波波源S1和S2的振幅分别为2A和A,某时刻它们形成的波峰和波谷分别由实线和虚线表示.下列说法正确的是( )
如图,两列水波波源S1和S2的振幅分别为2A和A,某时刻它们形成的波峰和波谷分别由实线和虚线表示.下列说法正确的是( )| A. | 两列波在相遇区域发生干涉 | |
| B. | 波谷和波谷相遇处位移为零 | |
| C. | A点的位移始终为零 | |
| D. | 此刻A点和B点的位移大小分别是A和3A |
17. 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带负电的质点仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 该质点在M点的电势能大于在N点的电势能 | |
| C. | 该质点在M点的动能大于在N点的动能 | |
| D. | 该质点在M点的加速度小于在N点的加速度 |
14.下列说法正确的是( )
| A. | 温度是分子平均动能的宏观标志,所以两个物体只要温度相等,那么他们分子的平均速率就相等 | |
| B. | 在自然界能的总量是守恒的,所以不存在能源危机 | |
| C. | 热力学第一定律也可表述为第一类永动机不可能制成 | |
| D. | 热力学第二定律可描述为“不可能使热量由低温物体传递到高温物体” | |
| E. | 质量相同且温度也相同的两种不同理想气体,其内能一定相同 |
18. 如图为自行车传动装置机械简图,在自行车匀速行进过程中,链轮A和飞轮C的加速度之比ωA:ωC=1:3,飞轮C和后轮B的边缘点线速度之比为vC:vB=1:12,则:( )
如图为自行车传动装置机械简图,在自行车匀速行进过程中,链轮A和飞轮C的加速度之比ωA:ωC=1:3,飞轮C和后轮B的边缘点线速度之比为vC:vB=1:12,则:( )
 如图为自行车传动装置机械简图,在自行车匀速行进过程中,链轮A和飞轮C的加速度之比ωA:ωC=1:3,飞轮C和后轮B的边缘点线速度之比为vC:vB=1:12,则:( )
如图为自行车传动装置机械简图,在自行车匀速行进过程中,链轮A和飞轮C的加速度之比ωA:ωC=1:3,飞轮C和后轮B的边缘点线速度之比为vC:vB=1:12,则:( )| A. | rA:rC=3:1 | |
| B. | rB:rC=4:1 | |
| C. | ωA:ωB=1:4 | |
| D. | 轮A和轮B的边缘点线速度之比vA:vB=1:4 |
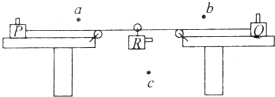 某同学利用图示装置验证系统机械能守恒定律,图中P、Q、R是三个完全相同的物块,P、Q用细绳连接,放在光滑水平桌面上,物块R与轻质滑轮连接,放在两定滑轮的中间.a、b、c是三个光电门,调整三个光电门的位置,能实现同时遮光.整个装置无初速度释放,已知P、Q、R经过三个光电门的遮光时间分别为t1、t2、t3,R的遮光片到c的距离为H,三个遮光片的宽度均为x.
某同学利用图示装置验证系统机械能守恒定律,图中P、Q、R是三个完全相同的物块,P、Q用细绳连接,放在光滑水平桌面上,物块R与轻质滑轮连接,放在两定滑轮的中间.a、b、c是三个光电门,调整三个光电门的位置,能实现同时遮光.整个装置无初速度释放,已知P、Q、R经过三个光电门的遮光时间分别为t1、t2、t3,R的遮光片到c的距离为H,三个遮光片的宽度均为x.