题目内容
倾角为θ=37°的固定光滑斜面,高为h=3m,左侧有质量为m=1kg的小球置光滑的水平面上,在斜面右侧放置有块竖直挡板高为H=4m,现给对小球一个水平向右的大小为 的初速度,(不计小球与斜面底端的接触处碰撞能量损失和空气阻力).则挡板距离斜面右侧的距离在哪些范围内可使小球击中挡板?(sin37°=0.6,cos37°=0.8,取g=10m/s2,
的初速度,(不计小球与斜面底端的接触处碰撞能量损失和空气阻力).则挡板距离斜面右侧的距离在哪些范围内可使小球击中挡板?(sin37°=0.6,cos37°=0.8,取g=10m/s2, ,
, )
)
【答案】分析:小球由斜面最低点运动到最高点的过程,运用动能定理求出小球到达斜面最高点时的速度,将此速度分解为水平和竖直两个方向.小球离开斜面后做斜抛运动,水平方向做匀速运动,竖直方向做竖直上抛运动,由运动学公式得到水平和竖直两个方向的位移与时间的表达式,要使小球能击中挡板,竖直位移y≤H-h=1m,得到抛体运动的轨迹方程,由数学知识可求出挡板距离斜面右侧的距离范围.
解答: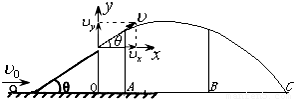 解:小球由斜面最低点运动到最高点时,由动能定理可得:
解:小球由斜面最低点运动到最高点时,由动能定理可得: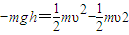
解得: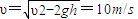
在斜面最高点时运动分解如图所示: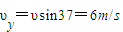 ;
;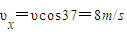
则可得小球在竖直方向的运动方程为: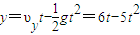 …①
…①
小球沿水平方向的运动方程为:x=υxt=8t…②
则小球能击中挡板时,由上可知y≤H-h=1m…③
由①③联立解得:当t1=0.2s,t2=1s
结合抛体运动的轨迹方程和图中可知,挡板在OA和BC之间时,能被小球击中.
则由②可得
xOA=υxt1=1.6m…④
xOB=υxt2=8m…⑤
取抛出点为坐标原点为,则C点对应的纵坐标为y=-3m,
结合①解得t3=1.6s
则由②可得xOC=υxt3=12.8m…⑥
结合④⑤⑥可知,挡板在距离斜面左端距离为0~1.6m或8~12.8m之间时,可使小球击中挡板.
答:挡板在距离斜面左端距离为0~1.6m或8~12.8m之间时,可使小球击中挡板.
点评:本题中涉及斜抛运动,其研究方法是运动的合成和分解,本题的解题关键是运用数学知识解决轨迹问题.
解答:
 解:小球由斜面最低点运动到最高点时,由动能定理可得:
解:小球由斜面最低点运动到最高点时,由动能定理可得: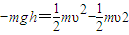
解得:
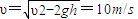
在斜面最高点时运动分解如图所示:
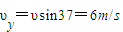 ;
;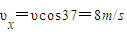
则可得小球在竖直方向的运动方程为:
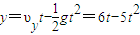 …①
…①小球沿水平方向的运动方程为:x=υxt=8t…②
则小球能击中挡板时,由上可知y≤H-h=1m…③
由①③联立解得:当t1=0.2s,t2=1s
结合抛体运动的轨迹方程和图中可知,挡板在OA和BC之间时,能被小球击中.
则由②可得
xOA=υxt1=1.6m…④
xOB=υxt2=8m…⑤
取抛出点为坐标原点为,则C点对应的纵坐标为y=-3m,
结合①解得t3=1.6s
则由②可得xOC=υxt3=12.8m…⑥
结合④⑤⑥可知,挡板在距离斜面左端距离为0~1.6m或8~12.8m之间时,可使小球击中挡板.
答:挡板在距离斜面左端距离为0~1.6m或8~12.8m之间时,可使小球击中挡板.
点评:本题中涉及斜抛运动,其研究方法是运动的合成和分解,本题的解题关键是运用数学知识解决轨迹问题.

练习册系列答案
相关题目
 将一个矩形金属线框折成“L”形框架abcdefa(∠dcb=∠efa=90°),置于倾角为α=37°的斜面上,ab边与斜面底边MN平行,如图所示.ab=bc=cd=de=ef=fa=0.2m,线框总电阻为R=0.02Ω,ab边和de边的质量均为m=0.01kg,其余四边的质量均不计,框架可绕过c、f点的固定轴转动.现从t=0时刻开始沿斜面向上加一随时间均匀增加的、范围足够大的匀强磁场,磁感强度与时间关系为B=kt(k=0.5T/s),磁场方向与cdef面垂直.
将一个矩形金属线框折成“L”形框架abcdefa(∠dcb=∠efa=90°),置于倾角为α=37°的斜面上,ab边与斜面底边MN平行,如图所示.ab=bc=cd=de=ef=fa=0.2m,线框总电阻为R=0.02Ω,ab边和de边的质量均为m=0.01kg,其余四边的质量均不计,框架可绕过c、f点的固定轴转动.现从t=0时刻开始沿斜面向上加一随时间均匀增加的、范围足够大的匀强磁场,磁感强度与时间关系为B=kt(k=0.5T/s),磁场方向与cdef面垂直. 山地滑雪是人们喜爱的一项体育运动.一滑雪坡由斜坡AB和半径R=5m的圆弧面BC组成,圆弧面和斜面相切于B,与水平面相切于C,如图所示.竖直台阶CD高度差为h=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力,sin37°=0.6,cos37°=0.8).已知运动员经过C点时的速度大小14m/s,求:
山地滑雪是人们喜爱的一项体育运动.一滑雪坡由斜坡AB和半径R=5m的圆弧面BC组成,圆弧面和斜面相切于B,与水平面相切于C,如图所示.竖直台阶CD高度差为h=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力,sin37°=0.6,cos37°=0.8).已知运动员经过C点时的速度大小14m/s,求: (2012?黄埔区模拟)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=37°的斜面AB和水平面BC以及另一个倾角仍为θ=37°的斜面DE三部分组成.已知水平面BC长为0.4m,D位置在C点的正下方,CD高为H=0.9m,E点与C点等高,P为斜面DE的中点;小球与接触面间的动摩擦因数均为μ=0.15,重力加速度g取10m/s2.现将此小球离BC水平面400h高处的斜面上静止释放,小球刚好能落到P点(sin37°=0.6,cos37°=0.8).
(2012?黄埔区模拟)如图所示,一个固定在竖直平面内的轨道,有倾角为θ=37°的斜面AB和水平面BC以及另一个倾角仍为θ=37°的斜面DE三部分组成.已知水平面BC长为0.4m,D位置在C点的正下方,CD高为H=0.9m,E点与C点等高,P为斜面DE的中点;小球与接触面间的动摩擦因数均为μ=0.15,重力加速度g取10m/s2.现将此小球离BC水平面400h高处的斜面上静止释放,小球刚好能落到P点(sin37°=0.6,cos37°=0.8).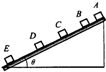 一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物体下滑加速度
一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物体下滑加速度 山地滑雪是人们喜爱的一项体育运动.一滑雪坡由斜面AB和圆弧面BC组成,BC圆弧面和斜面相切于B,与水平面相切于C,如图所示,AC竖直高度差hl=9.8m,竖直台阶CD高度差为h2=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).
山地滑雪是人们喜爱的一项体育运动.一滑雪坡由斜面AB和圆弧面BC组成,BC圆弧面和斜面相切于B,与水平面相切于C,如图所示,AC竖直高度差hl=9.8m,竖直台阶CD高度差为h2=5m,台阶底端与倾角为37°斜坡DE相连.运动员连同滑雪装备总质量为80kg,从A点由静止滑下通过C点后飞落到DE上(不计空气阻力和轨道的摩擦阻力,g取10m/s2,sin37°=0.6,cos37°=0.8).