题目内容
3. 如图所示,xoy平面的一、二、三象限内存在垂直纸面向外,磁感应强度B=1T的匀强磁场,ON为处于y轴负方向的弹性绝缘薄挡板,长度为9m,M点为x轴正方向上一点,OM=3m,现有一个比荷大小为$\frac{q}{m}$=1.0C/kg可视为质点带正电的小球(重力不计)从挡板下端N处小孔以不同的速度向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过M点,则小球射入的速度大小可能是( )
如图所示,xoy平面的一、二、三象限内存在垂直纸面向外,磁感应强度B=1T的匀强磁场,ON为处于y轴负方向的弹性绝缘薄挡板,长度为9m,M点为x轴正方向上一点,OM=3m,现有一个比荷大小为$\frac{q}{m}$=1.0C/kg可视为质点带正电的小球(重力不计)从挡板下端N处小孔以不同的速度向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过M点,则小球射入的速度大小可能是( )| A. | 3m/s | B. | 3.75m/s | C. | 4m/s | D. | 5m/s |
分析 由题意,带正电的小球从挡板下端N处小孔向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,所以小球运动的圆心的位置一定在y轴上,然后由几何关系得出可能的碰撞的次数,以及圆心可能的位置,然后由比较公式即做出判定.
解答 解:由题意,小球运动的圆心的位置一定在y轴上,所以小球做圆周运动的半径r一定要大于等于3m,而ON=9m<3r,所以小球最多与挡板ON碰撞一次,碰撞后,第二个圆心的位置在O点的上方.也可能小球与挡板ON没有碰撞,直接过M点.
由于洛伦兹力提供向心力,所以:qvB=$m\frac{{v}_{\;}^{2}}{r}$得:
$v=\frac{qBr}{m}$ ①
1.若小球与挡板ON碰撞一次,则轨迹可能如图1,

设OO′=s,由几何关系得:r2=OM2+s2=9+s2 ②
3r-9=s ③
联立②③得:r1=3m;r2=3.75m
分别代入①得:
${v}_{1}^{\;}=\frac{q}{m}•B{r}_{1}^{\;}=1×1×3m/s=3m/s$
${v}_{2}^{\;}=\frac{q}{m}•B{r}_{2}^{\;}=1×1×3.75=3.75m/s$
2.若小球没有与挡板ON碰撞,则轨迹如图2,设OO′=s,由几何关系得:
${r}_{3}^{2}=O{M}_{\;}^{2}+{x}_{\;}^{2}=9+{x}_{\;}^{2}$ ④
x=9-r3 ⑤
联立④⑤得:r3=5m
代入①得:${v}_{3}^{\;}=\frac{q}{m}•B{r}_{3}^{\;}=1×1×5=5m/s$
故选:ABD
点评 提供带电粒子在磁场中的圆周运动来考查牛顿第二定律,向心力公式,并突出几何关系在本题的应用,同时注重对运动轨迹的分析,利用圆的特性来解题是本题的突破口.

 重150N的光滑球A悬空靠在墙和木块B之间,木块B的重力为1500N,且静止在水平地板上,如图所示,则( )
重150N的光滑球A悬空靠在墙和木块B之间,木块B的重力为1500N,且静止在水平地板上,如图所示,则( )| A. | 墙所受压力的大小为150$\sqrt{3}$N | B. | 木块A对木块B压力的大小为150N | ||
| C. | 木块B所受摩擦力大小为150$\sqrt{3}$N | D. | 水平地板所受的压力为1500N |
 根据《日经新闻》的报道,日本将在2020年东京奥运会开幕之前使“无人驾驶”汽车正式上路并且投入运营.高度详细的3D地图技术能够为“无人驾驶”汽车提供大量可靠的数据,这些数据可以通过汽车内部的机器学习系统进行全面的分析,以执行不同的指令.如图所示为一段公路拐弯处的3D地图,你认为以下说法正确的是( )
根据《日经新闻》的报道,日本将在2020年东京奥运会开幕之前使“无人驾驶”汽车正式上路并且投入运营.高度详细的3D地图技术能够为“无人驾驶”汽车提供大量可靠的数据,这些数据可以通过汽车内部的机器学习系统进行全面的分析,以执行不同的指令.如图所示为一段公路拐弯处的3D地图,你认为以下说法正确的是( )| A. | 如果弯道是水平的,则“无人驾驶”汽车在拐弯时受到重力、支持力、摩擦力和向心力 | |
| B. | 如果弯道是水平的,则“无人驾驶”汽车在拐弯时收到的指令应让车速小一点,防止汽车作离心运动而发生侧翻 | |
| C. | 如果弯道是倾斜的,3D地图上应标出内(东)高外(西)低 | |
| D. | 如果弯道是倾斜的,3D地图上应标出外(西)高内(东)低 |
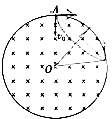 如图所示,在半径为R的圆形区域内有一磁感应强度方向垂直于纸面向里的匀强磁场,一质量为m且带正电的粒子(重力不计)以初速度v0从圆形边界上A点正对圆心射入该磁场区域,若该带电粒子在磁场中运动的轨迹半径为$\sqrt{3}$R,则下列说法中正确的是( )
如图所示,在半径为R的圆形区域内有一磁感应强度方向垂直于纸面向里的匀强磁场,一质量为m且带正电的粒子(重力不计)以初速度v0从圆形边界上A点正对圆心射入该磁场区域,若该带电粒子在磁场中运动的轨迹半径为$\sqrt{3}$R,则下列说法中正确的是( )| A. | 该带电粒子在磁场中将向左偏转 | |
| B. | 该带电粒子在磁场中运动的时间为$\frac{\sqrt{3}πR}{3{v}_{0}}$ | |
| C. | 该带粒子的轨迹圆弧对应的圆心角为30° | |
| D. | 若增大磁场的磁感应强度,则该带电粒子在磁场中运动的轨道半径将变大 |
 电阻R、电容C与一线圈连成闭合电路.条形磁铁静止于线圈的正上方,N极朝下,如图所示,现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向是从b到a,电容器上极板带负电.
电阻R、电容C与一线圈连成闭合电路.条形磁铁静止于线圈的正上方,N极朝下,如图所示,现使磁铁开始自由下落,在N极接近线圈上端的过程中,流过R的电流方向是从b到a,电容器上极板带负电.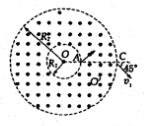 如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.
如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.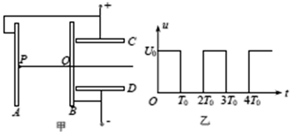 如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求:
如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求: