题目内容
15.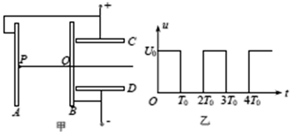 如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求:
如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求:(1)A、B板间的距离d1;
(2)粒子从D板边缘射出时速度方向与PQ延长线夹角的正切值;
(3)t=$\frac{{T}_{0}}{2}$时刻产生的粒子,从C、D板右侧射出时偏离PQ延长线的距离.
分析 (1)由运动情况结合运动学公式求得距离.
(2)因做类平抛运动,求出两方向的速度确定出偏角的正切值.
(3)先分段求解再求总偏离距离.
解答 解:(1)在 0-T1时间内,A、B间为匀强电场,粒子匀加速运动,设A、B板间的距离为d1,
则 ${a}_{1}=K\frac{{U}_{0}}{{d}_{1}}$ ${x}_{1}=\frac{1}{2}{a}_{1}{T}_{0}^{2}$
在T0-2T0时间内粒子做匀速运动x2=a1T0•T0
而x1+x2=d1整理得:${d}_{1}=\sqrt{\frac{3K{U}_{0}}{2}}{T}_{0}$
(2)粒子在CD板间运动时,沿平行于极板方向做匀速运动
vx=a1T0
沿垂直于极板方向做匀加速度运动,设CD板间的距离为d2,
${a}_{2}=K\frac{{U}_{0}}{{d}_{2}}$
$\frac{{d}_{2}}{2}=\frac{1}{2}{a}_{2}{T}_{0}^{2}$
vy=a2T0
则tanα=$\frac{{v}_{y}}{{v}_{x}}$=$\sqrt{\frac{3}{2}}$
(3)设粒子在2T0+t时刻到达Q,根据运动学公式
$\frac{1}{2}{a}_{1}(\frac{{T}_{0}}{2})^{2}+{a}_{1}(\frac{{T}_{0}}{2}){T}_{0}+{a}_{1}\frac{{T}_{0}}{2}t+\frac{1}{2}{a}_{1}$t2=d1
整理得t=$\frac{\sqrt{8}-1}{2}{T}_{0}$,因t<T0,所以粒子在2T0-3T0之间的某时刻经过Q,此时粒子的 速度大小
v=${a}_{1}(\frac{{T}_{0}}{2}+t)-\sqrt{2}{a}_{1}{T}_{0}$
设CD板长为L,由(2)知L=v0T0
所以粒子通过CD板间的时间为$△t=\frac{L}{v}$
整理得$△t=\frac{\sqrt{2}}{2}{T}_{0}$由于T0-t<△t<T0所以粒子在CD间运动过程中,沿垂直极板方向先以加速度a2匀加速运动 (T0-t)时间,再以速度a2(T0-t)时间,故从CD右侧飞出时偏离PQ延长线的距离为$y=\frac{1}{2}{a}_{2}({T}_{0}-t)^{2}+{a}_{2}({T}_{0}-t)_{\;}$(△t-(T0-t))
整理得:y=$\frac{18\sqrt{2}-25}{8}\sqrt{K{U}_{0}}{T}_{0}$
答:(1)A、B板间的距离为$\sqrt{\frac{3K{U}_{0}}{2}}{T}_{0}$
(2)粒子从D板边缘射出时速度方向与PQ延长线夹角的正切值为$\sqrt{\frac{3}{2}}$;
(3)t=$\frac{{T}_{0}}{2}$时刻产生的粒子,从C、D板右侧射出时偏离PQ延长线的距离为$\frac{18\sqrt{2}-25}{8}\sqrt{K{U}_{0}}{T}_{0}$
点评 本题带电粒子在周期性电场中运动问题,分析粒子的运动情况是关键,运用运动的分解法进行研究.


| A. | 甲表是安培表,R增大时量程增大 | B. | 甲表是安培表,R增大时量程减小 | ||
| C. | 乙表是伏特表,R减少时量程增大 | D. | 乙表是伏特表,R增大时量程减小 |
 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于P 点,轨道2、3相切于Q点,如图,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于P 点,轨道2、3相切于Q点,如图,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的速率小于在轨道1 上的速率 | |
| B. | 卫星在轨道1 上的速率大于在轨道2上Q点的速率 | |
| C. | 卫星在轨道1上经过P 点的加速度等于它在轨道2 上经过P 点时的加速度 | |
| D. | 卫星在轨道2上运行时的周期大于它在轨道3上运行时的周期 |
 如图所示,xoy平面的一、二、三象限内存在垂直纸面向外,磁感应强度B=1T的匀强磁场,ON为处于y轴负方向的弹性绝缘薄挡板,长度为9m,M点为x轴正方向上一点,OM=3m,现有一个比荷大小为$\frac{q}{m}$=1.0C/kg可视为质点带正电的小球(重力不计)从挡板下端N处小孔以不同的速度向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过M点,则小球射入的速度大小可能是( )
如图所示,xoy平面的一、二、三象限内存在垂直纸面向外,磁感应强度B=1T的匀强磁场,ON为处于y轴负方向的弹性绝缘薄挡板,长度为9m,M点为x轴正方向上一点,OM=3m,现有一个比荷大小为$\frac{q}{m}$=1.0C/kg可视为质点带正电的小球(重力不计)从挡板下端N处小孔以不同的速度向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电量不变,小球最后都能经过M点,则小球射入的速度大小可能是( )| A. | 3m/s | B. | 3.75m/s | C. | 4m/s | D. | 5m/s |
 一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )
一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )| A. | 质点E的振幅为零 | B. | 此波向x轴正方向传播 | ||
| C. | 质点C此时向y轴负方向运动 | D. | 质点C将比质点B先回到平衡位置 |
 如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )
如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )| A. | 粒子恰好不从cd边射出,轨道半径最大值为L | |
| B. | 粒子从ab边射出区域的最大长度为$\frac{2}{3}$L | |
| C. | 粒子恰好没有从ab边射出,该带电粒子在磁场中飞行的时间为$\frac{3πm}{5Bq}$ | |
| D. | 带电粒子从ad边射出,粒子入射时的最大速度为$\frac{BqL}{3m}$ |
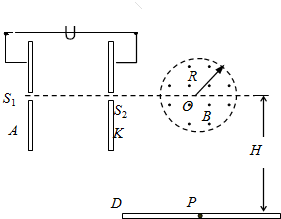 如图,在以O为圆心、半径R═10$\sqrt{3}$cm的圆形区域内,有一个方向垂直于纸面向外的水平匀强磁场.磁感应强度B=0.1T,两金属极板A、K竖直平行放置,A、K间的电压U=900V,S1、S2为A、K板上的两个小孔,且S1、S2跟O处于垂直极板的同一水平线上,在O点下方距离O点H=3R处有一块足够长的荧光屏D放置在水平面内,比荷为$\frac{q}{m}$=2.0×106C/kg的离子流由S1进入电场后,之后沿S2、O连线离开电场并随后射入磁场,通过磁场后落到荧光屏上.离子进入电场的初速度、离子的重力,离子之间的相互作用力均可忽略不计.
如图,在以O为圆心、半径R═10$\sqrt{3}$cm的圆形区域内,有一个方向垂直于纸面向外的水平匀强磁场.磁感应强度B=0.1T,两金属极板A、K竖直平行放置,A、K间的电压U=900V,S1、S2为A、K板上的两个小孔,且S1、S2跟O处于垂直极板的同一水平线上,在O点下方距离O点H=3R处有一块足够长的荧光屏D放置在水平面内,比荷为$\frac{q}{m}$=2.0×106C/kg的离子流由S1进入电场后,之后沿S2、O连线离开电场并随后射入磁场,通过磁场后落到荧光屏上.离子进入电场的初速度、离子的重力,离子之间的相互作用力均可忽略不计. 在竖直平面内有一矩形区域ABCD,AB边长L,AD边长2L,F为AD边中点,G为BC边中点,线段FG将ABCD分成两个场区.如图所示,场区Ⅰ内有一竖直向下的匀强电场,场区Ⅱ内有方向大小未知的匀强电场(图中未画出)和方向垂直ABCD平面内的匀强磁场,一个质量为m,电量为+q的带电小球以平行于BC边的速度v从AB边的中点P进入场区Ⅰ,从FG边飞出场区Ⅰ时速度方向改变了37°,小球进入场区Ⅱ做匀速圆周运动,求:
在竖直平面内有一矩形区域ABCD,AB边长L,AD边长2L,F为AD边中点,G为BC边中点,线段FG将ABCD分成两个场区.如图所示,场区Ⅰ内有一竖直向下的匀强电场,场区Ⅱ内有方向大小未知的匀强电场(图中未画出)和方向垂直ABCD平面内的匀强磁场,一个质量为m,电量为+q的带电小球以平行于BC边的速度v从AB边的中点P进入场区Ⅰ,从FG边飞出场区Ⅰ时速度方向改变了37°,小球进入场区Ⅱ做匀速圆周运动,求: 如图所示,在一平面直角坐标系所确定的平面内存在着两个匀强磁场区域,以一,三象限角平分线为界.上方区域磁场B1,垂直纸面向外,下方区城磁场B2,也垂直纸面向外.且有B1=2B2=2B(B为已知量).在边界上坐标为(l,l)的位置有一粒子发射源S.不断向Y轴负方向发射各种速率的带电粒子.所有粒子带电均为+q,质量均为m.这些粒子只受磁场力在纸面内运动,试问:
如图所示,在一平面直角坐标系所确定的平面内存在着两个匀强磁场区域,以一,三象限角平分线为界.上方区域磁场B1,垂直纸面向外,下方区城磁场B2,也垂直纸面向外.且有B1=2B2=2B(B为已知量).在边界上坐标为(l,l)的位置有一粒子发射源S.不断向Y轴负方向发射各种速率的带电粒子.所有粒子带电均为+q,质量均为m.这些粒子只受磁场力在纸面内运动,试问: