题目内容
6.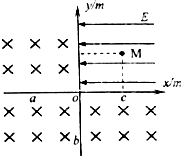 如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,沿x轴负方向的匀强电场,其余三个象限分布着垂直纸面向里的匀强磁场.现从电场中的M(0.5,0.5),点由静止释放一比荷为$\frac{q}{m}$=2×104C/kg的带正电微粒,重力不计.已知粒子第一次进入磁场后经坐标轴上的a、b、c点后再次垂直进入电场,其中oa=ob=oc=0.5m,求:
如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,沿x轴负方向的匀强电场,其余三个象限分布着垂直纸面向里的匀强磁场.现从电场中的M(0.5,0.5),点由静止释放一比荷为$\frac{q}{m}$=2×104C/kg的带正电微粒,重力不计.已知粒子第一次进入磁场后经坐标轴上的a、b、c点后再次垂直进入电场,其中oa=ob=oc=0.5m,求:(1)匀强磁场的磁感应强度
(2)带电微粒第二次进入磁场时的位置坐标y.
分析 (1)根据动能定理求出粒子进入匀强磁场的速度,结合几何关系求出粒子在磁场中做圆周运动的半径,结合半径公式求出匀强磁场的磁感应强度.
(2)带电微粒第二次进入磁场前做类平抛运动,根据牛顿第二定律和运动学公式求出带电微粒第二次进入磁场时的位置坐标y.
解答 解:(1)设带电粒子第一次进入磁场中的速度为v,半径为R,第一次在电场中加速,由动能定理得
$qEx=\frac{1}{2}m{v}^{2}$,
带电粒子在磁场中做圆周运动,有:qvB=$m\frac{{v}^{2}}{R}$
由题设几何关系可得R=0.5m.
代入数据解得B=0.1T.
(2)依题意粒子在磁场中刚好运动3/4圆周后,从点(0.5,0)处垂直电场做类平抛运动,设再次从y轴进入磁场的位置坐标为(0,y),则由类平抛运动运动规律得:
y=vt,
x=$\frac{1}{2}a{t}^{2}$,
根据牛顿第二定律得,a=$\frac{qE}{m}$
代入数据解得y=1.0m.
答:(1)匀强磁场的磁感应强度为0.1T;
(2)带电微粒第二次进入磁场时的位置坐标y为1.0m.
点评 本题考查了带电粒子在磁场和电场中的运动,理清粒子在整个过程中的运动规律是解决本题的关键,粒子在匀强磁场中运动,一般采用半径公式、周期公式和几何关系进行求解;垂直电场方向进入电场,做类平抛运动,一般采用动力学知识,运用运动合成分解进行求解.

练习册系列答案
相关题目
16. 如图所示为汽车的加速度a和车速的倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,最大车速为30m/s,则( )
如图所示为汽车的加速度a和车速的倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,最大车速为30m/s,则( )
 如图所示为汽车的加速度a和车速的倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,最大车速为30m/s,则( )
如图所示为汽车的加速度a和车速的倒数$\frac{1}{v}$的关系图象.若汽车质量为2×103kg,它由静止开始沿平直公路行驶,且行驶中阻力恒定,最大车速为30m/s,则( )| A. | 汽车匀加速的加速度为3m/s2 | |
| B. | 汽车所受阻力为4×103N | |
| C. | 汽车在车速为15m/s时,功率为6×104W | |
| D. | 汽车匀加速所需时间为5s |
17.下列关于曲线运动的说法中正确的是( )
| A. | 做曲线运动的物体速度方向时刻改变 | |
| B. | 物体只在重力作用下不可能做曲线运动 | |
| C. | 物体做曲线运动时加速度不可能是恒定的 | |
| D. | 做曲线运动的物体受到的合外力可能为零 |
14.物理学重视逻辑,崇尚理性,其理论总是建立在对事实观察的基础上.下列说法不正确的是( )
| A. | 天然放射现象说明原子核内部是有结构的 | |
| B. | 热电子束射到晶体上产生衍射图样说明实物粒子具有波动性 | |
| C. | 电子的发现使人们认识到原子具有核式结构 | |
| D. | 波尔的原子模型假定核外电子的轨道是不连续的 |
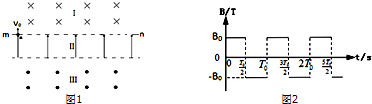
 如图所示,一枚炸弹自水平匀速飞行的战机上自由释放,不计空气阻力,在炸弹下落的过程中,在以下选项中△p-t图象及$\frac{△p}{△t}$-t图象正确的是(取竖直向下为正方向)( )
如图所示,一枚炸弹自水平匀速飞行的战机上自由释放,不计空气阻力,在炸弹下落的过程中,在以下选项中△p-t图象及$\frac{△p}{△t}$-t图象正确的是(取竖直向下为正方向)( )



 如图甲所示,光滑平台右侧与长为L=3.6m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=6m/s滑上木板,恰好滑到木板右端停止.求:
如图甲所示,光滑平台右侧与长为L=3.6m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=6m/s滑上木板,恰好滑到木板右端停止.求:
 三维弹球(3D Pinball)是Window里面附带的一款使用键盘操作的电脑游戏,小王同学受此启发,在学校组织的趣味运动会上,为大家提供了一个类似的弹珠游戏.如图所示,将一质量为m=0.1kg的小弹珠(可视为质点)放在O点,用弹簧装置将其弹出,使其沿着光滑的半圆形轨道OA和AB进入水平桌面BC,从C点水平抛出.已知半圆型轨道OA和AB的半径分别为r=0.2m,R=0.4m,BC为一段长为L=2.0m的粗糙水平桌面,小弹珠与桌面间的动摩擦因数为μ=0.4,放在水平地面的矩形垫子DEFG的DE边与BC垂直,C点离垫子的高度为h=0.8m,C点离DE的水平距离为x=0.6m,垫子的长度EF为1m,g=10m/s2.求:
三维弹球(3D Pinball)是Window里面附带的一款使用键盘操作的电脑游戏,小王同学受此启发,在学校组织的趣味运动会上,为大家提供了一个类似的弹珠游戏.如图所示,将一质量为m=0.1kg的小弹珠(可视为质点)放在O点,用弹簧装置将其弹出,使其沿着光滑的半圆形轨道OA和AB进入水平桌面BC,从C点水平抛出.已知半圆型轨道OA和AB的半径分别为r=0.2m,R=0.4m,BC为一段长为L=2.0m的粗糙水平桌面,小弹珠与桌面间的动摩擦因数为μ=0.4,放在水平地面的矩形垫子DEFG的DE边与BC垂直,C点离垫子的高度为h=0.8m,C点离DE的水平距离为x=0.6m,垫子的长度EF为1m,g=10m/s2.求: