题目内容
18.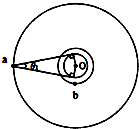 我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,如图为“天链一号”卫星a、赤道平面内的低轨道卫星b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,己知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )
我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,如图为“天链一号”卫星a、赤道平面内的低轨道卫星b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,己知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )| A. | 张角θ1和θ2满足sinθ2=4sinθ1 | |
| B. | 卫星a与卫星b运动的加速度之比4:1 | |
| C. | 卫星b每次在盲区运行的时间$\frac{({θ}_{1}+{θ}_{2})T}{14π}$ | |
| D. | 卫星a运行一周将与地心及卫星b共线14次 |
分析 根据几何关系求解张角θ1和θ2满足的关系,由万有引力提供向心力,列式求解卫星b的周期.卫星间的通讯信号视为沿直线传播,由几何关系得到卫星b在盲区有两个边缘相对于地球的张角,再求解在盲区运行的时间.
解答 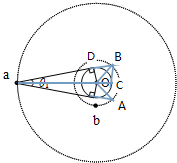 解:A、设卫星a、b的轨道半径分别为${r}_{1}^{\;}$和${r}_{2}^{\;}$,地球半径为R,
解:A、设卫星a、b的轨道半径分别为${r}_{1}^{\;}$和${r}_{2}^{\;}$,地球半径为R,
由几何关系得$sin\frac{{θ}_{1}^{\;}}{2}=\frac{R}{{r}_{1}^{\;}}$,$sin\frac{{θ}_{2}^{\;}}{2}=\frac{R}{{r}_{2}^{\;}}$
由题${r}_{1}^{\;}=4{r}_{2}^{\;}$,则得$4sin\frac{{θ}_{1}^{\;}}{2}=sin\frac{{θ}_{2}^{\;}}{2}$,由数学知识$sin{θ}_{2}^{\;}≠4sin{θ}_{1}^{\;}$,故A错误;
B、根据向心加速度$a=\frac{GM}{{r}_{\;}^{2}}$,得$\frac{{a}_{1}^{\;}}{{a}_{2}^{\;}}=\frac{{r}_{2}^{2}}{{r}_{1}^{2}}=\frac{1}{16}$,故B错误;
C、如图,a、b是卫星盲区两个边缘位置,由几何知识可得$∠AOB={θ}_{1}^{\;}+{θ}_{2}^{\;}$,则$(\frac{2π}{\frac{T}{8}}-\frac{2π}{T})t=∠AOB={θ}_{1}^{\;}+{θ}_{2}^{\;}$,解得,b每次在盲区运行的时间为$t=\frac{({θ}_{1}^{\;}+{θ}_{2}^{\;})}{14π}T$,故C正确;
D、根据$T=2π\sqrt{\frac{{r}_{\;}^{3}}{GM}}$,则周期之比为$\frac{{T}_{a}^{\;}}{{T}_{b}^{\;}}=\sqrt{\frac{{4}_{\;}^{3}}{{1}_{\;}^{3}}}=8$
设每隔时间t,a、b共线一次,$({ω}_{b}^{\;}-{ω}_{a}^{\;})t=π$,所以$t=\frac{π}{{ω}_{b}^{\;}-{ω}_{a}^{\;}}$=$\frac{{T}_{a}^{\;}{T}_{b}^{\;}}{2({T}_{a}^{\;}-{T}_{b}^{\;})}$
则故b运动一周的过程中,卫星a运行一周将与地心及卫星b共线的次数为:
$n=\frac{{T}_{a}^{\;}}{t}$=$\frac{2({T}_{a}^{\;}-{T}_{b}^{\;})}{{T}_{b}^{\;}}=14$,故D正确;
故选:CD
点评 本题既要掌握卫星问题的基本思路:万有引力提供向心力,更重要的是画出示意图,运用几何知识解答.

| A. | 布朗运动是悬浮微粒的无规则运动,温度越高、微粒越大,运动越显著 | |
| B. | 任何物体的内能都不能为零 | |
| C. | 分子间距离r<r0时,分子间表现为斥力,随着r的减小,分子势能Ep增大 | |
| D. | 一定质量的气体,保持压强不变,可以同时升高温度和减小体积; | |
| E. | 液晶像液体一样具有流动性,而其光学性质和某些晶体相似具有各向异性 | |
| F. | 液体饱和汽的压强称为饱和汽压,大小随温度和体积的变化而变化 |
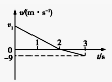 将一质量为1kg的物体以一定的初速度竖直向上抛出,假设物体在运动过程中所受空气阻力的大小恒定不变,其速度-时间图象如图所示,取重力加速度g=10m/s2,则( )
将一质量为1kg的物体以一定的初速度竖直向上抛出,假设物体在运动过程中所受空气阻力的大小恒定不变,其速度-时间图象如图所示,取重力加速度g=10m/s2,则( )| A. | 物体下降过程中的加速度大小为9m/s2 | |
| B. | 物体受到的阻力为1N | |
| C. | 图中v1=10m/s | |
| D. | 图中v1=22m/s |
 如图所示A、B两物体用轻弹簧连接,放在光滑水平面上,物体A紧靠竖直墙.若推物体B使弹簧压缩,然后由静止释放,物体B开始运动,则( )
如图所示A、B两物体用轻弹簧连接,放在光滑水平面上,物体A紧靠竖直墙.若推物体B使弹簧压缩,然后由静止释放,物体B开始运动,则( )| A. | 弹簧第一次恢复到原长时,物体A开始加速,B继续加速 | |
| B. | 弹簧第一次拉伸至最长时,两个物体的速度一定相同 | |
| C. | 弹簧第二次恢复到最长时,两个物体的速度一定反向 | |
| D. | 弹簧再次压缩到最短时,物体A的速度可能为零 |

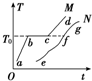 如图所示,两条曲线分别表示晶体和非晶体在一定压强下的熔化过程,图中横轴表示时间t,纵轴表示温度T.从图中可以确定曲线M表示晶体(填“晶体”或“非晶体”),T0表示晶体的熔点,曲线M的bc段表示熔化过程,此过程中,物体吸收(填“吸收”或“放出”)热量,内能增加(填“增加”、“减小”或“不变”).
如图所示,两条曲线分别表示晶体和非晶体在一定压强下的熔化过程,图中横轴表示时间t,纵轴表示温度T.从图中可以确定曲线M表示晶体(填“晶体”或“非晶体”),T0表示晶体的熔点,曲线M的bc段表示熔化过程,此过程中,物体吸收(填“吸收”或“放出”)热量,内能增加(填“增加”、“减小”或“不变”).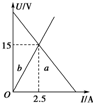 如图所示,图线a是某一蓄电池组的伏安特性曲线,图线b是一定值电阻的伏安特性曲线.将蓄电池组与该定值电阻连成闭合回路,若已知该蓄电池组的内阻为2.0Ω.则:
如图所示,图线a是某一蓄电池组的伏安特性曲线,图线b是一定值电阻的伏安特性曲线.将蓄电池组与该定值电阻连成闭合回路,若已知该蓄电池组的内阻为2.0Ω.则: