题目内容
5.如图为接在50Hz低压交流电源上的打点计时器在纸带做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的记数点,但第3个记数点的点迹不清楚,无法确定位置.
由图数据可求得:
(1)该物体的加速度为2.0m/s2(保留2位有效数字)
(2)第2个记数点与第3个记数点的距离约为5.00cm(保留3位有效数字)
(3)打第3个点时该物体的速度为0.60m/s.(保留2位有效数字)
分析 物体做的是匀变速直线运动,(1)求解加速度时首先想到的应该是逐差法,但是只有两组数据,所以要找两组数据之间的关系,推论xm-xn=(m-n)at2可提供这两组数据与加速度的关系,应用这个推论即可.
(2)第2、3两点间的距离对应的应该为x2,要想得到x2必须找他和已知量的关系,x2-x1=at2提供了这个关系.
(3)为了让结果更精确,我们需要用上这两组数据,而这两组数据只能求他们自己这段位移中的平均速度,v3需要找它与这两个平均速度的关系:而v3对应的时刻为这两个速度所对应的时间的中间时刻,可由v${\;}_{\frac{t}{2}}$=$\frac{{v}_{0}+v}{2}$求出.
解答 解:(1)设1、2间的位移为x1,2、3间的位移为x2,3、4间的位移为x3,4、5间的位移为x4;
因为周期为T=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s;
由匀变速直线运动的推论xm-xn=(m-n)at2得:
x4-x1=3at2带入数据得:
(9.00-3.00)×10-2=3a×0.12
解得:a=2.0m/s2.
(2)第3个记数点与第2个记数点的距离即为x2,由匀变速直线运动的推论:x2-x1=at2得:
x2=x1+at2带入数据得:
x2=3.00×10-2+2.0×0.12=0.05m
即为:5.00cm.
(3)为了让结果更精确,我们需要用上这两组数据:设1、2两点间中间时刻的速度为v1,4、5点间的中间时刻的速度速度为v2
则:v1=$\frac{{x}_{1}}{T}$,v2=$\frac{{x}_{4}}{T}$ 带入数据得:
得:v1=0.3m/s,v2=0.9m/s
因为点3为v1v2所对应的时间的中间时刻,所以由v${\;}_{\frac{t}{2}}$=$\frac{{v}_{0}+v}{2}$得:
v3=$\frac{{v}_{1}+{v}_{2}}{2}$,带入数据得:
v3=$\frac{0.3+0.9}{2}$ m/s=0.60m/s
故打3这个点时的速度为:0.60m/s.
故答案为:
(1)2.0;
(2)5.00;
(3)0.60.
点评 匀变速直线运动的推论,无论是实验还是平时计算上用处很多需要熟练掌握.处理实验数据时还应该注意单位换算和有效数字的保留.

| A. | 三者都只受万有引力的作用,万有引力都提供向心力 | |
| B. | 月球的向心加速度大于地球同步卫星的向心加速度 | |
| C. | 地球同步卫星的角速度与静止在地球赤道上的物体的角速度相同 | |
| D. | 地球同步卫星相对地心的线速度与静止在地球赤道上的物体相对地心的线速度大小相等 |
| A. | vt一定大于v0 | B. | v0是初速度,是瞬时速度 | ||
| C. | vt可能小于v0 | D. | at指t时间内的速度变化量 |
| A. | 电子伏是能量的单位 | |
| B. | 1J=1.60×1019eV | |
| C. | 只要是均匀的球形带电体,不管球的大小,都能被看成点电荷 | |
| D. | 带电体间的距离比它们本身的大小大得多,以至于带电体的形状和大小对它们间相互作用力的影响可忽略不计时,带电体就可以视为点电荷 |
| A. | 布朗运动虽然不是液体分子的运动,但是它说明液体分子永不停息地做无规则运动 | |
| B. | 只要知道某种液体的摩尔体积和该液体分子的质量,就可以计算出阿伏伽德罗常数 | |
| C. | 完全失重状态下悬浮的水滴呈球形,是液体表面张力作用的结果 | |
| D. | 分子间的作用力表现为引力时,若分子间的距离增大,则分子力减小,分子势能增大 | |
| E. | 单晶体冰糖磨碎后熔点不会发生变化 |
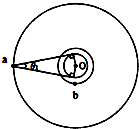 我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,如图为“天链一号”卫星a、赤道平面内的低轨道卫星b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,己知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )
我国的“天链一号”卫星是地球同步卫星,可为中低轨道卫星提供数据通讯,如图为“天链一号”卫星a、赤道平面内的低轨道卫星b、地球的位置关系示意图,O为地心,地球相对卫星a、b的张角分别为θ1和θ2(θ2图中未标出),卫星a的轨道半径是b的4倍,己知卫星a、b绕地球同向运行,卫星a的周期为T,在运行过程中由于地球的遮挡,卫星b会进入卫星a通讯的盲区,卫星间的通讯信号视为沿直线传播,信号传输时间可忽略.下列分析正确的是( )| A. | 张角θ1和θ2满足sinθ2=4sinθ1 | |
| B. | 卫星a与卫星b运动的加速度之比4:1 | |
| C. | 卫星b每次在盲区运行的时间$\frac{({θ}_{1}+{θ}_{2})T}{14π}$ | |
| D. | 卫星a运行一周将与地心及卫星b共线14次 |
