题目内容
8. 如图所示,一个质量为m、带有电荷量为-q的小物体,可以在水平轨道Ox上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿Ox轴正方向,小物体以速度v0从距固定墙x0处沿Ox轨道运动,运动时受到大小不变的摩擦力Ff作用,且Ff<qE.设小物体与墙碰撞时不损失机械能,且电荷量保持不变,则它在停止运动前所通过的总路程x=$\frac{2qE{x}_{0}+m{{v}_{0}}^{2}}{2{F}_{f}}$.
如图所示,一个质量为m、带有电荷量为-q的小物体,可以在水平轨道Ox上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿Ox轴正方向,小物体以速度v0从距固定墙x0处沿Ox轨道运动,运动时受到大小不变的摩擦力Ff作用,且Ff<qE.设小物体与墙碰撞时不损失机械能,且电荷量保持不变,则它在停止运动前所通过的总路程x=$\frac{2qE{x}_{0}+m{{v}_{0}}^{2}}{2{F}_{f}}$.
分析 由于Ff<qE,物体最终停止在固定墙处;在整个运动的过程中,阻力一直做负功,电场力最终做正功,根据动能定理求出通过的总路程.
解答 解:电场力做功与路径无关,滑动摩擦力始终做负功,由动能定理得:
qEx0-Ffx=0-$\frac{1}{2}$mv${\;}_{0}^{2}$,
解得x=$\frac{2qE{x}_{0}+m{{v}_{0}}^{2}}{2{F}_{f}}$.
故答案为:$\frac{2qE{x}_{0}+m{{v}_{0}}^{2}}{2{F}_{f}}$.
点评 物块经过若干次碰撞做往复运动最后停止,只能通过动能定理求运动的总路程;注意克服摩擦力做功等于摩擦力乘以相对路程,电场力做功与路径无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16. 如图所示,空间有一匀强电场方向水平向右,在竖直平面内,一带电粒子以v0的速度从A点进入该空间后沿直线运动到B点,这一过程中能量变化情况是( )
如图所示,空间有一匀强电场方向水平向右,在竖直平面内,一带电粒子以v0的速度从A点进入该空间后沿直线运动到B点,这一过程中能量变化情况是( )
 如图所示,空间有一匀强电场方向水平向右,在竖直平面内,一带电粒子以v0的速度从A点进入该空间后沿直线运动到B点,这一过程中能量变化情况是( )
如图所示,空间有一匀强电场方向水平向右,在竖直平面内,一带电粒子以v0的速度从A点进入该空间后沿直线运动到B点,这一过程中能量变化情况是( )| A. | 动能减少、重力势能增加,电势能减少 | |
| B. | 动能减少、重力势能增加,电势能增加 | |
| C. | 动能不变、重力势能增加,电势能减少 | |
| D. | 动能增加、重力势能增加,电势能减少 |
3. 如图所示,在光滑绝缘的斜面上有一质量为m、带电量为+q的小球,为了使它能在斜面上做匀速圆周运动,除了用一丝线拴住外,必须加一个电场,该电场的方向和大小为( )
如图所示,在光滑绝缘的斜面上有一质量为m、带电量为+q的小球,为了使它能在斜面上做匀速圆周运动,除了用一丝线拴住外,必须加一个电场,该电场的方向和大小为( )
 如图所示,在光滑绝缘的斜面上有一质量为m、带电量为+q的小球,为了使它能在斜面上做匀速圆周运动,除了用一丝线拴住外,必须加一个电场,该电场的方向和大小为( )
如图所示,在光滑绝缘的斜面上有一质量为m、带电量为+q的小球,为了使它能在斜面上做匀速圆周运动,除了用一丝线拴住外,必须加一个电场,该电场的方向和大小为( )| A. | 方向与斜面成30°角向下,大小为$\frac{mg}{q}$ | |
| B. | 方向沿斜面向上,大小为$\frac{mgsin30°}{q}$ | |
| C. | 方向垂直斜面向下,大小为$\frac{mgsin30°}{q}$ | |
| D. | 方向竖直向下,大小为$\frac{mg}{q}$ |
13. 如图所示的匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°角,ab=4cm,bc=10cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-6J,则( )
如图所示的匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°角,ab=4cm,bc=10cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-6J,则( )
 如图所示的匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°角,ab=4cm,bc=10cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-6J,则( )
如图所示的匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°角,ab=4cm,bc=10cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-6J,则( )| A. | 将此电荷从b移到c电场力做功5×10-6J | |
| B. | 将此电荷从b移到c电场力做功1×10-5J | |
| C. | ac间电势差为200V | |
| D. | ac间电势差为450V |
18.物体沿一直线运动,下列说法中正确的是( )
| A. | 物体在第一秒末的速度是5m/s,则物体在第一秒内的位移一定是5m | |
| B. | 物体在第一秒内的平均速度是5m/s,则物体在第一秒内的位移一定是5m | |
| C. | 物体在某段时间内的平均速度是5m/s,则物体在每一秒内的位移都是5m | |
| D. | 物体在某段位移内的平均速度是5m/s,则物体在经过这段位移一半时的速度不一定是5m/s |
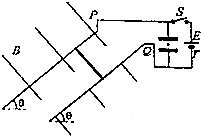 如图所示,两平行光滑金属导轨P、Q相距L=0.1m,导轨平面与水平面的夹角为θ=37°,导轨上端接有如图所示的电路,直流电源电动势为E,内阻r=0.2Ω,水平放置的平行金属板电容器两极板间距d=0.01m,将长L=0.1m、质量m1=0.02kg,电阻R=0.4Ω的金属杆ab垂直于导轨P、Q放置在导轨上,同时在金属杆ab所在空间加上方向垂直于导轨平面的匀强磁场(方向为标出),当开关S闭合时,电容器两极板间有一质量m2=4×10-7kg、电荷量q=2×10-8C的带负电微粒恰好静止平衡,且金属杆ab也静止在导轨上,不计导轨和导线的电阻,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求;
如图所示,两平行光滑金属导轨P、Q相距L=0.1m,导轨平面与水平面的夹角为θ=37°,导轨上端接有如图所示的电路,直流电源电动势为E,内阻r=0.2Ω,水平放置的平行金属板电容器两极板间距d=0.01m,将长L=0.1m、质量m1=0.02kg,电阻R=0.4Ω的金属杆ab垂直于导轨P、Q放置在导轨上,同时在金属杆ab所在空间加上方向垂直于导轨平面的匀强磁场(方向为标出),当开关S闭合时,电容器两极板间有一质量m2=4×10-7kg、电荷量q=2×10-8C的带负电微粒恰好静止平衡,且金属杆ab也静止在导轨上,不计导轨和导线的电阻,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求;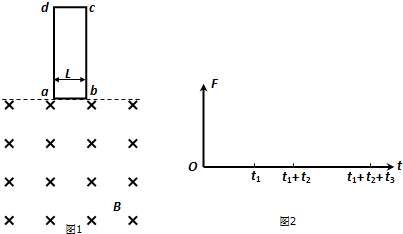
 如图所示,在E=103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=0.4m,一带电荷的小滑块质量为m=0.04kg,电荷量为q,小滑块与水平轨道间的动摩因数μ=0.2,g取10m/s2,求:
如图所示,在E=103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=0.4m,一带电荷的小滑块质量为m=0.04kg,电荷量为q,小滑块与水平轨道间的动摩因数μ=0.2,g取10m/s2,求: