题目内容
15. 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )| A. | 当ω=$\sqrt{\frac{g}{2l}}$时,细绳的拉力为0 | |
| B. | 当ω=$\sqrt{\frac{3g}{4l}}$时,物块与转台间的摩擦力为0 | |
| C. | 当ω=$\sqrt{\frac{4g}{3l}}$时,细绳的拉力大小为$\frac{4}{3}$mg | |
| D. | 当ω=$\sqrt{\frac{g}{l}}$时,细绳的拉力大小为$\frac{1}{3}$mg |
分析 对物体受力分析知物块离开圆盘前合力F=f+Tsinθ=$m\frac{{v}^{2}}{r}$;N+Tcosθ=mg,根据题目提供的条件,结合临界条件分析即可.
解答 解:A、当转台的角速度比较小时,物块只受重力、支持力和摩擦力,当细绳恰好要产生拉力时:
$μmg={mω}_{1}^{2}(lsinθ)$,
解得:${ω}_{1}=\sqrt{\frac{2g}{3l}}$,由于$\sqrt{\frac{g}{2l}}<\sqrt{\frac{2g}{3l}}$,所以当ω=$\sqrt{\frac{g}{2l}}$时,细线中张力为零.故A正确;
B、随速度的增大,细绳上的拉力增大,当物块恰好要离开转台时,物块受到重力和细绳的拉力的作用,则:$mgtanθ={mω}_{2}^{2}(lsinθ)$
解得:${ω}_{2}=\sqrt{\frac{2\sqrt{3}g}{3l}}$,由于${ω}_{1}<\sqrt{\frac{3g}{4l}}<{ω}_{2}$,所以当ω=$\sqrt{\frac{3g}{4l}}$时,物块与转台间的摩擦力不为零.故B错误;
D、当ω=$\sqrt{\frac{4g}{3l}}$>ω2时,小球已经离开转台,细绳的拉力与重力的合力提供向心力,则:$mgtanα=m(\sqrt{\frac{4g}{3l}})^{2}lsinα$
解得:cosα=$\frac{3}{4}$,故$F=\frac{mg}{cosα}=\frac{4}{3}mg$.故C正确.
D、由于${ω}_{1}<\sqrt{\frac{g}{l}}<{ω}_{2}$,由牛顿第二定律:$f+Fsinθ=m(\sqrt{\frac{g}{l}})^{2}lsinθ$,因为压力小于mg,所以$f<\frac{1}{3}mg$,解得:F>$\frac{1}{3}$mg.故D错误;
故选:AC
点评 此题考查牛顿运动定律的应用,注意临界条件的分析,至绳中出现拉力时,摩擦力为最大静摩擦力;转台对物块支持力为零时,N=0,f=0.题目较难,计算也比较麻烦.

| A. | A车在匀速过程中与B车相遇 | B. | A、B相遇时速度相同 | ||
| C. | 相遇时A车做匀速运动 | D. | 两车不可能相遇 |
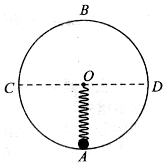 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )| A. | 当v0较小时,小球可能会离开圆轨道 | |
| B. | 若在$\sqrt{2gR}$<v0<$\sqrt{5gR}$则小球会在B、D间脱离圆轨道 | |
| C. | 只要v0>$\sqrt{4gR}$,小球就能做完整的圆周运动 | |
| D. | 只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差与v0无关 |
| A. | 安培通过实验发现了通电导线对磁体有作用力,首次揭示了电与磁的联系 | |
| B. | 洛伦兹认为安培力是带电粒子所受磁场力的宏观表现,并提出了著名的洛伦兹力公式 | |
| C. | 奥斯特首先提出了磁场对运动电荷有力作用 | |
| D. | 法拉第根据通电螺线管的磁场和条形磁铁的磁场的相似性,提出了分子电流假说 |
| A. | 2N,水平向左 | B. | 2N,水平向右 | C. | 12N,水平向右 | D. | 8N,水平向右 |
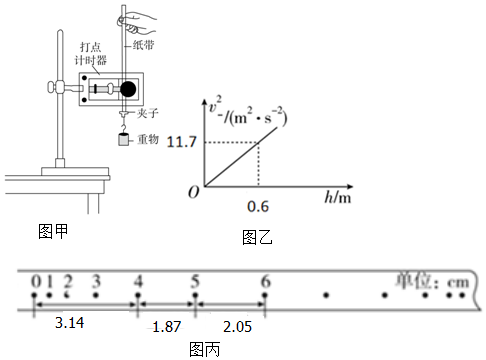


 由实验测得某弹簧所受弹力F和弹簧的长度L的关系图象如图所示,求:
由实验测得某弹簧所受弹力F和弹簧的长度L的关系图象如图所示,求: