题目内容
3.用如图所示实验装置验证机械能守恒定律,重物m从高处由静止开始下落,拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律.图甲中给出的是实验中获取的一条纸带;0是打下的第一个点,电源的频率为50HZ,计数点间的距离如图所示.已知m=2000g,则 (g取9.8m/s2,所有结果均保留三位有效数字)
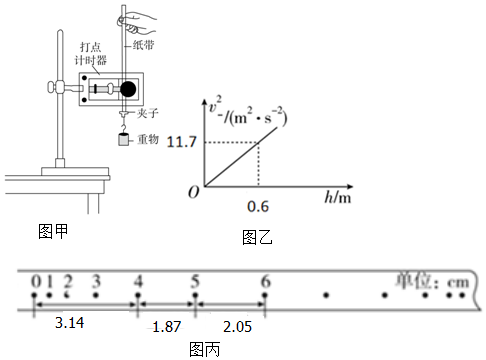
(1)在纸带上打下计数点5时的速度v5=0.980m/s;
(2)在打点0~5过程中系统动能的增量△Ek=0.960J,重力势能的减少量△Ep=0.982J,
(3)运用机械能守恒定律结论和该实验装置,还可以测量该地的重力加速度,若某同学作出v2h图象如图乙所示,则当地的实际重力加速度g=9.75m/s2.
分析 (1)根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点5的瞬时速度.
(2)根据计数点5的瞬时速度得出动能的增加量,根据下降的高度求出重力势能的减小量.
(3)根据机械能守恒得出v2-h的关系式,结合图线的斜率求出当地的重力加速度.
解答 解:(1)计数点5的瞬时速度${v}_{5}=\frac{{x}_{46}}{2T}=\frac{(1.87+2.05)×1{0}^{-2}}{0.04}$m/s=0.980m/s.
(2)在打点0~5过程中系统动能的增量△Ek=$\frac{1}{2}m{{v}_{5}}^{2}=\frac{1}{2}×2×0.98{0}^{2}$≈0.960J,重力势能的减小量$△{E}_{p}=mgh=2×9.8×(3.14+1.87)×1{0}^{-2}$≈0.982J.
(3)根据机械能守恒得,$mgh=\frac{1}{2}m{v}^{2}$,则v2=2gh,可知图线的斜率k=2g=$\frac{11.7}{0.6}$,解得g=9.75m/s2.
故答案为:(1)0.980,(2)0.960,0.982,(3)9.75.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度,从而得出动能的增加量,会根据下降的高度求解重力势能的减小量,对于图线问题,一般的解题思路是得出物理量间的关系式,结合图线的斜率或截距进行求解.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13.在“探究小车速度随时间变化规律”的实验中,打点计时器使用的交流电源的频率为50Hz,记录小车运动的纸带如图所示,在纸带上选择6个计数点A、B、C、D、E、F、G相邻两计数点之间还有四个点未画出.

(1)根据学过的知识可以求出小车在D点的速度为vD=0.560m/s(结果保留三位有效数字).
(2)以打A点时为计时起点,建立v-t坐标系如图所示,请在图中作出小车运动的速度与时间的关系图线:

| VB | VC | VD | VE | VF | |
| 数值(m/s) | 0.400 | 0.49 | 0.640 | 0.721 |
(2)以打A点时为计时起点,建立v-t坐标系如图所示,请在图中作出小车运动的速度与时间的关系图线:
14.一物体做直线运动的速度时间函数图象如图所示,则以下说法中错误的是( )


| A. | 该物体一直做加速运动 | |
| B. | 0~1s的加速度与1~2s的加速度大小相等,方向相同 | |
| C. | 该物体第1s时,运动方向变向 | |
| D. | 在第1s时,物体的速度为0,但是加速度不为零 |
18. 如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )
如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )
 如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )
如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )| A. | △p=6kgm/s,方向水平向左 | B. | △p=6kgm/s,方向水平向右 | ||
| C. | △p=2kgm/s,方向水平向左 | D. | △p=2kgm/s,方向水平向右 |
8.下列几组物理量中全部为矢量的是一组( )
| A. | 时间、位移、速度 | B. | 速度、速率、位移 | ||
| C. | 路程、时刻、速率 | D. | 位移、瞬时速度、加速度 |
15. 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )
 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )| A. | 当ω=$\sqrt{\frac{g}{2l}}$时,细绳的拉力为0 | |
| B. | 当ω=$\sqrt{\frac{3g}{4l}}$时,物块与转台间的摩擦力为0 | |
| C. | 当ω=$\sqrt{\frac{4g}{3l}}$时,细绳的拉力大小为$\frac{4}{3}$mg | |
| D. | 当ω=$\sqrt{\frac{g}{l}}$时,细绳的拉力大小为$\frac{1}{3}$mg |

