题目内容
6.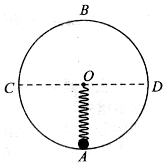 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )| A. | 当v0较小时,小球可能会离开圆轨道 | |
| B. | 若在$\sqrt{2gR}$<v0<$\sqrt{5gR}$则小球会在B、D间脱离圆轨道 | |
| C. | 只要v0>$\sqrt{4gR}$,小球就能做完整的圆周运动 | |
| D. | 只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差与v0无关 |
分析 AB、在轨道的任意位置对小球受力分析,比较弹簧的弹力于重力在半径方向上的分力的大小,即可得知选项AB的正误.
C、利用机械能守恒定律可解的小球做圆周运动时在最低点的速度,由此可判知选项C的正误.
D、根据向心力的公式分别列出在最高点和最低点赶到对小球的压力,结合小球在运动过程中机械能守恒,即可推导出压力之差的表达式,从而可知选项D的正误.
解答 解:AB、因弹簧的劲度系数为k=$\frac{mg}{R}$,原长为L=2R,所以小球始终会受到弹簧的弹力作用,大小为F=K(L-R)=KR=mg,方向始终背离圆心,无论小球在CD以上的哪个位置速度为零,重力在沿半径方向上的分量都小于等于弹簧的弹力(在CD以下,轨道对小球一定有指向圆心的支持力),所以无论v0多大,小球均不会离开圆轨道,故A错误,B错误.
C、小球在运动过程中只有重力做功,弹簧的弹力和轨道的支持力不做功,机械能守恒,当运动到最高点速度为零,在最低点的速度最小,有:$\frac{1}{2}m{{v}_{0}}^{2}=2mgR$,所以只要${v}_{0}>\sqrt{4gR}$,小球就能做完整的圆周运动,故C正确.
D、在最低点时,设小球受到的支持力为N,有:N-kR-mg=$m\frac{{{v}_{0}}^{2}}{R}$,解得:N=2mg+$m\frac{{{v}_{0}}^{2}}{R}$…①
运动到最高点时受到轨道的支持力最小,设为N′,设此时的速度为v,由机械能守恒有:$\frac{1}{2}m{{v}_{0}}^{2}=2mgR+\frac{1}{2}m{v}^{2}$…②
此时合外力提供向心力,有:N′-KR+mg=$m\frac{{v}^{2}}{R}$…③
联立②③解得:N′=$m\frac{{{v}_{0}}^{2}}{R}-4mg$…④
联立①④得压力差为:△N=6mg,与初速度无关,故D正确.
故选:CD.
点评 该题涉及到的考点较多,解答中要注意一下几点:
1、正确的对物体进行受力分析,计算出沿半径方向上的合外力,利用向心力公式进行列式.
2、注意临界状态的判断,知道临界状态下受力特点和运动的特点.
3、熟练的判断机械能守恒的条件,能利用机械能守恒进行列式求解.


(1)为了研究加速度和质量的关系,在实验中必须采用控制变量法,应保持拉力F不变,用砂桶及砂所受的重力作为小车所受拉力,图(b)为某次实验得到的纸带,实验数据如图,图中相邻计数点之间还有4个点未画出,根据纸带可求出小车的加速度大小为0.64 m/s2.(保留三位有效数字)
(2)在本次实验中,实验小组通过改变小车质量共做了8组实验,得到下表所示的实验数据,通过分析表中数据,你得出的结论是:在小车所受外力不变的条件下,加速度与质量成反比例关系.
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/(m•s-2) | 0.633 | 0.572 | 0.497 | 0.418 | 0.332 | 0.250 | 0.167 | 0.101 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
(3)在某次实验中为研究加速度和力的关系,根据测得的多组数据可画出a-F关系图线,如图(c)所示.此图线的AB段明显偏离直线,造成此误差的主要原因是C
| A.小车与木板之间存在摩擦 | B.木板保持了水平状态 |
| C.所挂砂桶及砂的总质量太大 | D.所用小车的质量太大 |

| A. | 该物体一直做加速运动 | |
| B. | 0~1s的加速度与1~2s的加速度大小相等,方向相同 | |
| C. | 该物体第1s时,运动方向变向 | |
| D. | 在第1s时,物体的速度为0,但是加速度不为零 |
| A. | 物体从静止开始下落的运动就是自由落体运动 | |
| B. | 如果空气阻力比重力小得多,空气阻力可以忽略不计,这时由静止开始下落的运动可以看做自由落体运动 | |
| C. | 跳伞运动员从飞机上由静止开始下落,打开降落伞以前的运动看做自由落体运动,打开降落伞以后的运动不是自由落体运动 | |
| D. | 一雨滴从屋顶落下,途中经过一个窗子,雨滴经过窗子的这一段运动是自由落体运动 |
 如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )
如图所示,一个质量是2kg的钢球,以2m/s的初速度水平向右射到竖直的墙壁上.碰撞后水平向左弹回,速度为1m/s.选取水平向右为正方向,下列关于钢球动量变化的大小和方向正确的是( )| A. | △p=6kgm/s,方向水平向左 | B. | △p=6kgm/s,方向水平向右 | ||
| C. | △p=2kgm/s,方向水平向左 | D. | △p=2kgm/s,方向水平向右 |
 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ=30°,此时绳伸直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω,重力加速度为g,则( )| A. | 当ω=$\sqrt{\frac{g}{2l}}$时,细绳的拉力为0 | |
| B. | 当ω=$\sqrt{\frac{3g}{4l}}$时,物块与转台间的摩擦力为0 | |
| C. | 当ω=$\sqrt{\frac{4g}{3l}}$时,细绳的拉力大小为$\frac{4}{3}$mg | |
| D. | 当ω=$\sqrt{\frac{g}{l}}$时,细绳的拉力大小为$\frac{1}{3}$mg |
 如图所示一物体做直线运动的速度时间图象,用v1、a1表示物体t1时间内地速度和加速度,v2、a2表示t1-t2时间内的速度和加速度,则由图可知( )
如图所示一物体做直线运动的速度时间图象,用v1、a1表示物体t1时间内地速度和加速度,v2、a2表示t1-t2时间内的速度和加速度,则由图可知( )| A. | v1和v2方向相同,a1和a2方向相同,a1>a2 | |
| B. | v1和v2方向相同,a1和a2方向相反,a1<a2 | |
| C. | v1和v2方向相反,a1和a2方向相同,a1>a2 | |
| D. | v1和v2方向相反,a1和a2方向相反,a1<a2 |