题目内容
16.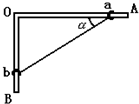 如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度$\frac{{v}_{a}}{{v}_{b}}$=( )
如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度$\frac{{v}_{a}}{{v}_{b}}$=( )| A. | tanα | B. | $\frac{1}{tanα}$ | C. | sinαcosα | D. | sin2α |
分析 将a、b的速度分解为沿绳子方向和垂直于绳子方向,抓住沿绳子方向的速度相等,结合平行四边形定则求出a的速度,继而可知各选项的正误.
解答 解:a、b的速度分解如图所示,环b沿绳子方向上的分速度为:v绳=vbsinα
环a沿绳子方向上的速度为:v绳′=vacosα
因为v绳=v绳′
则有:$\frac{{v}_{a}}{{v}_{b}}$=$\frac{sinα}{cosα}$=tanα.故A正确,BCD错误.
故选:A.
点评 该题是考察了关于连接体的问题,对于此类问题,找出相联系的两个物体的共同的物理量是解题的关键,解决本题的关键就是抓住沿绳子方向的分速度相等,然后再结合平行四边形定则即可求解.该题还要会熟练的应用三角函数解答相关的物理问题.

练习册系列答案
相关题目
6.关于斜抛运动,下列说法中错误的是( )
| A. | 斜抛运动是曲线运动 | B. | 斜抛运动是直线运动 | ||
| C. | 斜抛运动的最高点的速度为零 | D. | 斜抛运动是匀变速运动 |
7. 如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
 如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )| A. | 施加恒力后,物块与斜面间的弹力保持不变 | |
| B. | 施加恒力后,地面与斜面的支持力小于(M+m)g | |
| C. | 施加恒力后,物块与斜面间的摩擦力变小 | |
| D. | 施加恒力后,地面与斜面间的摩擦力大小为F |
4.关于机械波,下列说法中正确的是( )
| A. | 机械波的振幅与波源振动的振幅不相等 | |
| B. | 在波的传播过程中,介质中质点的振动频率等于波源的振动频率 | |
| C. | 在波的传播过程中,介质中质点的振动速度等于波的传播速度 | |
| D. | 在机械波的传播过程中,离波源越远的质点振动的周期越大 |
8.关于分子间作用力和分子势能,下列叙述正确的是( )
| A. | 分子间距增大时,分子间引力和斥力都减小 | |
| B. | 分子间距离减小时,分子间引力和斥力都增大 | |
| C. | 物体的体积减小时,内部分子势能可能减小 | |
| D. | 一个物体在分子间显引力时分子势能一定比显斥力时分子势能要多 | |
| E. | 当温度升高时,分子间的分子势能一定减小 |
5. 如图所示,磁感应强度大小为B的匀强磁场方向斜向右上方,与水平方向所夹的锐角为45°.将一个$\frac{3}{4}$金属圆环ab置于磁场中,圆环的圆心为O,半径为r,两条半径oa和0b相互垂直,且oa沿水平方向.当圆环中通以电流I时,圆环受到的安培力大小为( )
如图所示,磁感应强度大小为B的匀强磁场方向斜向右上方,与水平方向所夹的锐角为45°.将一个$\frac{3}{4}$金属圆环ab置于磁场中,圆环的圆心为O,半径为r,两条半径oa和0b相互垂直,且oa沿水平方向.当圆环中通以电流I时,圆环受到的安培力大小为( )
 如图所示,磁感应强度大小为B的匀强磁场方向斜向右上方,与水平方向所夹的锐角为45°.将一个$\frac{3}{4}$金属圆环ab置于磁场中,圆环的圆心为O,半径为r,两条半径oa和0b相互垂直,且oa沿水平方向.当圆环中通以电流I时,圆环受到的安培力大小为( )
如图所示,磁感应强度大小为B的匀强磁场方向斜向右上方,与水平方向所夹的锐角为45°.将一个$\frac{3}{4}$金属圆环ab置于磁场中,圆环的圆心为O,半径为r,两条半径oa和0b相互垂直,且oa沿水平方向.当圆环中通以电流I时,圆环受到的安培力大小为( )| A. | $\sqrt{2}BIr$ | B. | $\frac{3}{2}πBIr$ | C. | BIr | D. | 2BIr |